More slicing and dicing: the return of chapter 8

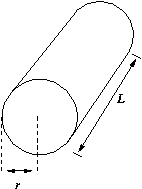
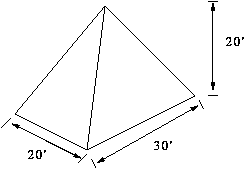
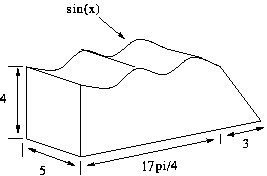
1. Consider each of the geometric figures below. Suppose that you wanted to determine the volume of each by integration. For each,
   1. Sketch on the diagram a representative slice of volume,
   2. Identify what the ``small dimension'' (dsomething) and independent variable in your integration are,
   3. Then find an equation for the volume of one slice of the figure, and finally
   4. Write an integral that would give the volume. Note that you do not have to evaluate this integral.

2. If the density of the earth as a function of the radial distance from the center of the earth is dens(r), write an integral for its mass. Pretend that the earth is spherical and that its radius is R_E.

3. Suppose that the density of information on a CD is given by dens(r) = (A / r) (bytes/cm²). Further, let the radius of a CD be R. (Both A and R are, of course, constants.) Write and evaluate an integral giving the total amount of information on the CD.

   

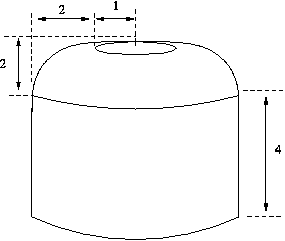
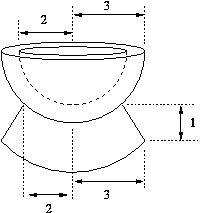
4. Consider the shape shown to the right. The top corners are rounded in the shape of a circle with the indicated radius. Find the volume of the shape.