a x + b y + c z = d and
z = d + m x + n y
a x + b y = c and
y = m x + b
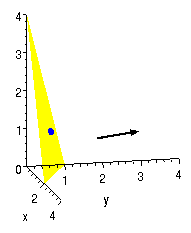 figure 1: normal vector and point, with and without plane.
figure 1: normal vector and point, with and without plane.
We find that different forms of the equation for a plane are useful in different situations, in the same way that the different forms of the equation for a line are useful in different situations. If we're given a slope and the y-intercept, we use the slope-intercept form of a line (the last one given above); if we have the slope and a point on the line, we use the point-slope form (the first, above). This same idea holds for planes. All three of the forms written above really are the same thing, just rendered in a different way. In the following we look at the same plane in each of these ways to see how they are equivalent.
Consider the plane with normal vector n = <2,4,1> that goes through the point P(1/2,1/2,1). The normal vector and point are shown without adding the plane and then adding the plane in figure 1 to the right. (Notice how the normal vector and the point do exactly determine the plane!) We can easily write the equation of the plane in all three ways:
Now suppose we were trying to find the plane through the points (0,0,4), (2,0,0) and (0,1,0). We can easily find the slope in the x and y direction as (change in z)/(change in x) and (change in z)/(change in y), respectively, using the first two and first and third points:
which leads us directly to the third of the forms of the equation for the plane above,
Now, how are the x-slope and y-slopes related to the coefficients of the normal vector? Going between the two forms
we see that the x-slope is m = -a/c and that the y-slope is n = -b/c. Is this the case for our specific example? Yup! a =2, b =4, and c =1.
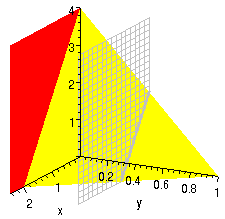
Ok, two more thoughts. Thought 1: This second example is pretty special: all of the points we were given were on the axes. When one of the points that we're given isn't the z-intercept, or when the points that we're given aren't in lines in the x and y directions, it's harder to just find the intercept and slopes. For example, if we're given three arbitrary points, say (1,3,-2), (-1,5,2) and (3,3,-8), we're sort of stuck and find the plane by getting two vectors, calculating a normal with the cross-product, etc.
Thought 2: is it obvious that the slopes in the x and y directions are constant for a plane? By the slope in the x-direction we mean the slope with the y coordinate fixed: we can illustrate this by drawing a plane with a fixed y coordinate and seeing what the slope of the line of intersection is. This is shown for two values of y in figure 2 to the left. (I've made the plane at y=0 red and that at y=0.5 grey and wire-frame, so that you can see through it.) Notice that in either case the slope of the line of intersection with the plane we're interested in is the same! So the x-slopes are in fact the same!
(How were the figures here generated? In Maple, with this maple worksheet.)