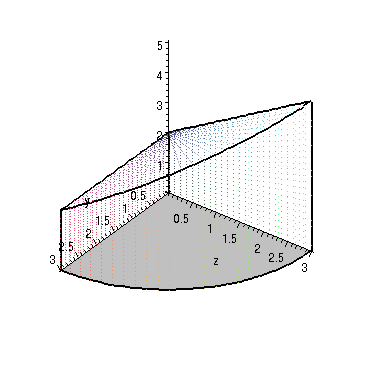
figure 1: the volume, showing the projection in the xy-plane
Here we consider integrating the function f(x,y,z) = xz over the volume inside x2 + y2 = 9, in the first octant, and under the plane z = y + 2. This region is shown to the right, below.
To set up the integral, we first need to decide on a coordinate system in which to work. Because this volume is defined on part of a cylindrical domain, and because it has straight (in z) sides, cylindrical coordinates are a good choice. The fact that the sides are vertical in z makes spherical coordinates less desirable. We could do it in rectangular coordinates, but in general with a region like this we expect the choice of cylindrical coordinates to be the best.
Next, we figure out the limits of integration. We'll do this two ways: first by thinking about the outer two limits of integration as a block, then by thinking about the inner two together.

Thinking about the outer two limits:
For the first of these, we think about the outer two variables first.
To do this, we choose which they'll be, and project the volume down
into the plane defined by those two variables. It makes sense here to
consider the r-theta plane, which is the same as the
xy-plane. This projection is shown in figure 1 to the
right.
We see that the projection is just a quarter circle of radius 3, so the limits on r and theta are 0 <= r <= 3 and 0 <= theta <= pi/2. Because both of these sets of limits are constant, it doesn't matter what order we put them in.
Finally, we need the limits for the inner variable, z. To find these, we think about any point in the projection and mentally extend lines in the z direction, seeing what the first and last values of z that are of interest are. To see this visually, click here a couple of times (click here to clear the arrows). Looking at these, we can see that the limits are 0 <= z <= y+2, or 0 <= z <= rsin(theta)+2. Thus, noting that f(x,y,z) = xz is the same as f(x,y,z) = r cos(theta) z, the final integral is
Thinking about fixing the outer variable:
For the second method, we're thinking about just one outer variable
first, and then find what "slices" of the volume look like when that
variable is held fixed. Here, either r or theta are the
best outer variables to consider, because with z fixed for
z <2 the slices have a different shape than when we
look at z >2. (Be sure you can see this by looking at
the figure.)
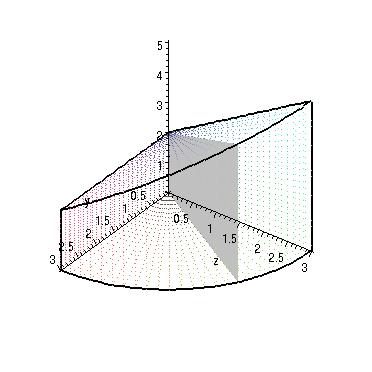
Let's think about theta as the outermost variable. Then a slice with theta fixed is shown in figure 2. The possible values for theta are any values in the first octant, so we need 0 <= theta <= pi/2.
Now in each slice, we want to think about forming a double integral in the remaining variables (r and z). We'll do this the same way we normally do: pick one for the outer variable, find the limits of integration for that, and then at each value of that outer variable figure out what the range of values for the inner variable is.
Let's think about r as the outer variable in the slice. Notice that no matter where we make the slice we always have 0 <= r <= 3, so this looks like a good choice for the outer slice variable. Then for each value of r, what does z do? As before, we think about taking any value of r in the slice (which can be at any of the possible values for theta, of course), and draw vertical lines to see what the values of z are click here a couple of times to see this visually (click here to clear the arrows). Looking at these, we can (again) see that the limits are 0 <= z <= rsin(theta)+2. Thus, the final integral becomes
which, because the outer two limits are constant, can be rewritten as
Evaluating the integral:
A quick integration. It's easiest to evaluate this
dz dtheta dr:
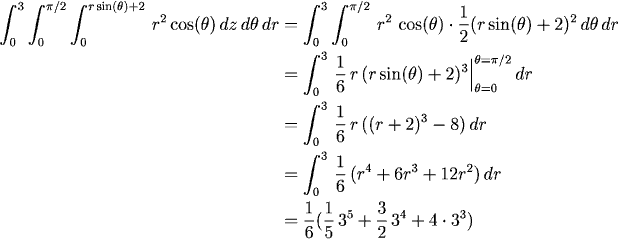
(Note that to do the integration in theta, we use the substitution u = (r sin(theta) + 2).
(How were the figures here generated? In Maple, with this maple worksheet.)