Ma316-001-F10 further explanation, §3.2
further explanation
existence and uniqueness
Consider two functions p(t) and q(t):
In[122]:=
Out[122]=
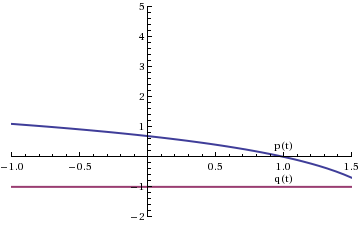
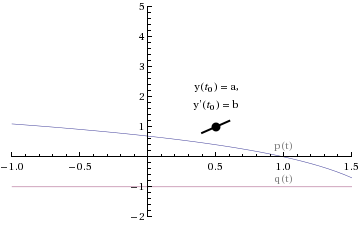
We know that the differential equation
y '' + p(t) y ' + q(t) y = 0,
with initial conditions
, 
In[145]:=
Out[145]=
Has a unique solution:
In[125]:=
Out[125]=
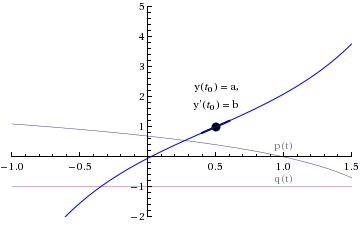
...as long as p(t) and q(t) are continuous
In[150]:=
Out[150]=
superposition of two (linearly independent) solutions can satisfy any initial condition
Now, suppose that we have two solutions, 
and 
, of
y '' + p(t) y ' + q(t) y = 0
In[177]:=
Out[177]=
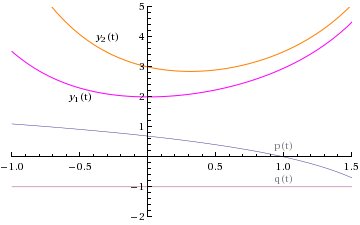
Then, if their Wronskian is non-zero at 
, given an initial condition there:
In[179]:=
Out[179]=
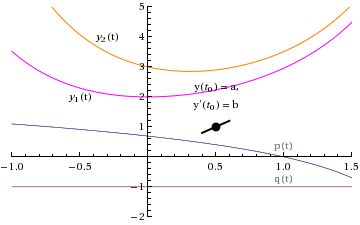
we can find a linear combination of 
and 
, 
that solves the initial value problem
y '' + p(t) y ' + q(t) y = 0, 
, 
:
In[202]:=
Out[202]=
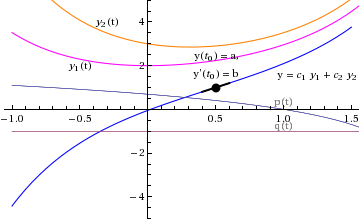
superposition of two (linearly independent) solutions gives the general solution
Now suppose that we are given any solution φ(t) of the differential equation
y '' + p(t) y ' + q(t) y = 0.
We want to show that we can write φ(t) as a linear combination of 
and 
, that is, that we can find a 
and 
so that
So, suppose that we have such a φ and that we know that at some point 
the Wronskian of 
and 
is non-zero.
In[210]:=
Out[210]=
Then, at 
, we know that φ(t) satisfies the initial value problem
That is, a solution to the differential equation with the initial conditions:
In[249]:=
Out[249]=
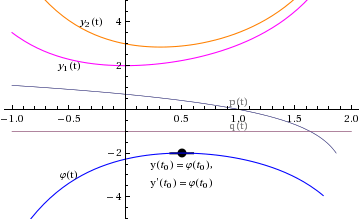
That is, we're solving the differential equation with these initial conditions:
In[251]:=
Out[251]=
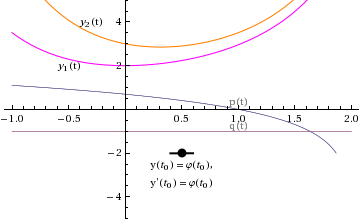
But, by the work in the previous section, we know that we can find a 
and a 
such that
satisfies the initial value problem
.
Thus:
In[246]:=
Out[246]=
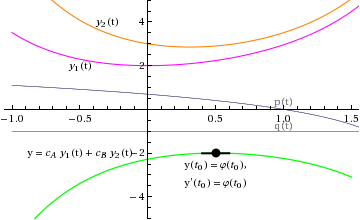
And the uniqueness theorem (the first section above) says that this solution is unique—that is, it must be the same function as the φ(t) that we started with:
In[248]:=
Out[248]=
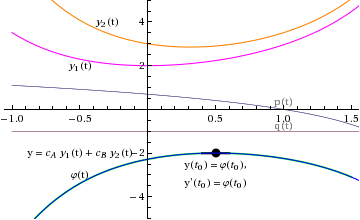
Thus, because we started off with the assumption that φ(t) was any solution to the differential equation, we've shown that the linear combination
is the general solution to the differential equation!
Super cool!
