MORE on Project 3
Ok, how do we deal with this thing? Hints: first
consider the dependence on phi, then that on theta1, then that on
theta2.
Dependence on phi
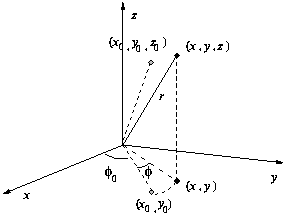 |
| Figure 1: Effect of changing phi |
See figure 1 to the right. Suppose that the elbow is initially
at a point (x0,y0,z0) and angle phi0, and then moves through an angle
phi. This causes a change in the position (x,y,z) as shown in the
figure. Clearly the z location doesn't change. Consider, therefore
only the x and y location. This is the projection onto the x-y plane;
write
x0 = (projected-length) cos(phi0) and
y0 = (projected-length) sin(phi0).
Then consider moving through the
angle phi:
x = (projected-length) cos(phi0 + phi)
and similarly for y. Using the trig identities
sin(a+b) = sin(a)cos(b) + sin(b)cos(a) and
cos(a+b) = cos(a)cos(b) - sin(a)sin(b),
and the fact that the z coordinate doesn't change, you should be able
to find the transformation matrix for this linear transformation.
Dependence on theta1
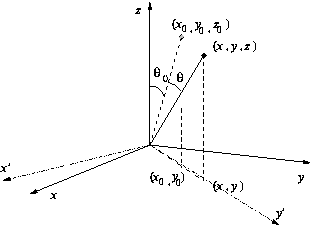 |
| Figure 2: Effect of changing theta1 |
Next, consider the effect of changing theta1, as shown in
figure 2 to the right. In this case, there is no change in the
position along an "x-prime" axis and there is change along a "y-prime"
and the z axes, as shown in the figure. So, if we were to first twist
the "y-prime" axis around to lie along either of the x or y axes, then
apply the (two-dimensional) transformation, then twist back, we'd be
set.
However, "twisting" the figure is just a transformation in phi, which
we know how to do (see above!). So, let phi_tot be the current value
of phi (which probably depends on x0 and y0, no?) -- then a
transformation through the angle -(phi_tot) will move the "y-prime"
axis to lie along the x-axis. In these coordinates, shown below, the
transformation is strictly two dimensional.
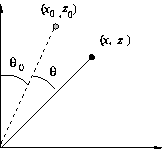
Therefore, in these coordinates, you can (easily!) find a
transformation matrix that accomplishes the rotation -- which
will change the x and z coordinates but not the y coordinate.
Then, transform (using your phi transformation) back through the angle
phi_tot to get the final point.
Dependence on theta2
Finally, what about theta2? This changes the position of the claw,
but not the position of the elbow. You should be able to use a very
similar matrix to that you found for theta1 here, with one difference:
it changes the position of the claw relative to the elbow.
The position of the claw relative to the elbow is just the difference
in the locations of the two, so that you should finish with something
like
(relative claw position) = Atheta2
(original relative claw position)
for some matrix Atheta2. You can
apply this transformation after having first applied the effect of the
phi and theta1 transformations to both the elbow and claw locations.
Last Modified: Thu May 6 01:36:13 CDT 1999
Project 3 help
Comments to
glarose@umich.edu



