Math 204--Calculus III: Project 2, Fall 1998
Costs of Production...
by Gavin LaRose
(glarose@umich.edu),
Nebraska Wesleyan University, November 1998
©1998 Gavin LaRose (glarose@umich.edu)
permission granted to use and distribute free in an academic setting.
-
- PostScript
version of project
Chemproc, Inc.
20000 Ryan-ears Blvd.
Lonlinc, SK 08685
4 November 1998
Sophisticated and Independent Mathematical Contractors (SIMaC), Inc.
Suite 5, Strawmarket Business Plaza
Lonlinc, SK 04685
Dear SIMaC:
Having received your report on the subject of our ``ChipLess''
microchip coating process, it is with considerable faith that we write
you again to request your assistance in our work on the marketing of
our latest product line expansion. This is to include two new
products, which we for the sake of proprietary secrecy shall refer to
as ``X'' and ``Y.'' As these are related they share some
production costs and resources, resulting in some difficulty in
ascertaining the optimum production quantities x and y of each,
and it is to determine this best marketing strategy that we are
contacting you.
We have found that, appropriately scaled, the production costs of
the manufacturing processes for these products is reasonably given by
C(x,y) = awx + bzy + xy,
where a and b are positive constants and w and
z are variables
that are dictated by costs of materials which are out of our control.
In the scaled variables, w and z vary between 0 and 1, and are
hypothesized to be either random values between these two extremes or
be most likely found near 0.75, with vanishing probabilies that they
will be equal to 0 or 1. As we are unable to vary our production in
response to the values of w and z, we need your analysis to treat
their possible values in the aggragate, and would like you to consider
both of the indicated possible models for their variation.
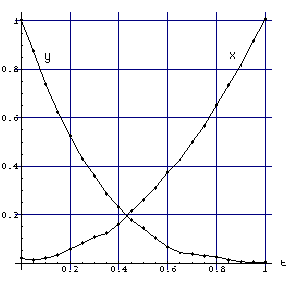We also find that the production quantities x and y are
constrained by the fact that they share common resources and are
influenced by interrelated market forces which, while they are again
beyond our control, are more predictable than the material costs noted
above. In a series of test marketing efforts we were able to vary the
sustainable production of x and y with time, finding that
they at maximum production behaved as shown in figure 1 to the right.
We believe this to indicate that x and y have some sort of direct
relationship that will constrain the production when we commence with
our long-term manufacturing and marketing of X and Y.
Insofar as possible we would like your analysis to be applicable for
general values of a and b, though we do expect that
a will be approximately 1 and b approximately 2.
We look forward to receiving your final report on or before the 30th
of November. To assure your success, we have again arranged for the
most estimable of mathematicians, Dr. P. Gavin LaRose, to answer any
questions you may have in the course of your investigation. Please
note, however, that he will unfortunately be unavailable to
assist with this project over the weekend of the 27th--29th of
November. You should plan on meeting with him before the week of
the 16th of November to verify your initial progress. We have also
made available, through him, a number of sample reports that may prove
useful as you develop your report.
Sincerely
E. Idu Pont
President, Chemproc, Inc.
eip:glr
Gavin's Calc III Project 2, Fall 1998
Last Modified: Thu Nov 12 22:36:41 CST 1998
Comments to
glarose@umich.edu