 and
and
Igor Kriz
Regular problems:
1.
The equations u=f(x,y), x=X(s,t) and y=Y(s,t) define u as a function of s and t, say u=F(s,t).
(a) Use an appropriate chain rule to express the partial derivatives of
 and
and ![]() in terms of
in terms of ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
(b) If f has continuous partial derivatives of second order, prove that
![]()
(c) Find similar formulas for the partial derivatives ![]() and
and ![]() .
.
2.
Let, in this problem, all functions have continuous partial derivatives
of all orders. For a function ![]() ,
a function
,
a function ![]() is given by
is given by

For a function ![]() where
where
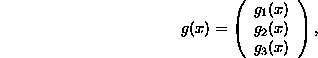
a function ![]() is given by
is given by
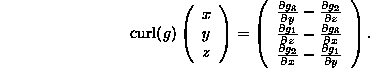
Finally, for a function ![]() where
where
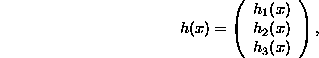
a function ![]() is given by
is given by
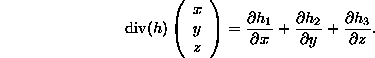
Prove that
![]()
![]()
3.
Let
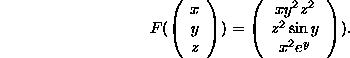
Calculate ![]() ,
, ![]() .
.
4.
Consider the function ![]() given by
given by
![]() . Determine the tangent plane to the graph of the
function f (which is a surface in
. Determine the tangent plane to the graph of the
function f (which is a surface in ![]() at a point
at a point
![]() .
.
Challenge problem:
5.
In the xz plane in ![]() , consider the circle C given by
th equation
, consider the circle C given by
th equation
![]()
Let M be the set obtained by rotating the circle C around the z axis (``the surface of a donut'').
(a) By finding local coordinate (=parametrizing) functions at all points, prove that M is a manifold.
(b) Using your parametrizations, calculate the vector tangent space to
M at a point 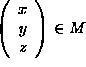 .
.
(c) Consider the function ![]() given as follows: Let
given as follows: Let
![]() be the image of C under rotation by the angle
be the image of C under rotation by the angle ![]() around the
z-axis. Then f maps
around the
z-axis. Then f maps ![]() to itself by rotating it by the
same angle
to itself by rotating it by the
same angle ![]() . (In measuring these angles, the angles from
the positive part of the x axis to the positive part of the y
axis and to the positive part of the z axis is considered to be
. (In measuring these angles, the angles from
the positive part of the x axis to the positive part of the y
axis and to the positive part of the z axis is considered to be
![]() .) Calculate Df.
.) Calculate Df.