
Igor Kriz
Regular problems:
1.
Compute the following integrals:
(a) 
(b) ![]()
(c) ![]() .
.
2.
Using integration of rational functions, compute:
(a) ![]()
(b) ![]() .
.
3.
Suppose ![]() is such that
||f(t)||=1 (the Euclidean norm
is such that
||f(t)||=1 (the Euclidean norm 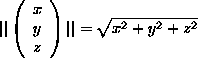 ) for every t.
Prove that
) for every t.
Prove that ![]() for every
for every ![]() .
.
4.
Define for ![]() ,
,
![]() .
Similarly, for
.
Similarly, for ![]() ,
,
 , let
, let 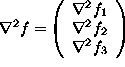 . (This is called the Laplacian.)
Prove that
. (This is called the Laplacian.)
Prove that
![]()
Challenge problems:
5.
Integrate:
(a) ![]()
(b) ![]()
(c) .
6.
Put f(0,0)=0, and
![]()
if ![]() . Prove that
. Prove that
(a) ![]() are continuous in
are continuous in ![]() ;
;
(b) ![]() and
and
![]() exist at every point of
exist at every point of ![]() and are continuous except at (0,0);
and are continuous except at (0,0);
(c) ![]()
![]()