Math 296 problems 3

Igor Kriz

1.

A school has three clubs, and each student is required to belong to exactly one club. One year the students switched club membership as follows:

Club A: 4/10 remain in A, switch to B, switch to C.

Club B: remain in B, switch to A, switch to C.

Club C: remain in C, switch to A, switch to B.

In the end, though, it turned out that the fraction of the student population in each club was unchanged. Find each of these fractions.

2.

Try these harder L'Hospital rule problems:

[Hint: convert each of these expressions into or .]

3.

The trace of a square matrix A, denoted by tr (A), is the sum of the diagonal entries of A. Prove that

(a) tr(AB)=tr(BA)

(b) is the sum of all squares of all entries of A. [Recall that the entry in the i-th row and j-th column of is the entry in the j-th row and i-the column of A.]

4.

Using elementary row operations, convert to reduced row echelon form:

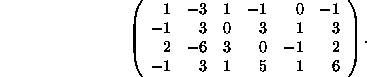
5.

Find an inverse of the following matrix, or conclude that one does not exist:

• About this document ...