Igor Kriz
1.
Consider a linear map 
fiven by f(x)=Ax, where A is an 
matrix. Prove that
the image of f, i.e. the set 
, is
equal to the column space Col(A).
2.
A problem in Chemistry:
The artificial sweetener Aspartame has chemical formula 
.
(a) Is it possible to prepare Aspartame from the following
ingredients with no byproducts:
Sucrose ( 
), glucose ( 
),
water ( 
), nitric acid ( 
) and nitrogen pentoxide
( 
)?
[In chemistry, a formula consists of names of atoms in the molecule;
the subscript stands for the number of atoms of an
element in the molecule. H is hydrogen, C is carbon, O is oxygen
and N is nitrogen. For example, a molecule of water has 2 atoms
of hydrogen and one atom of oxygen.]
(b) The molecules in (a) can be represented by
elements of 
where the coordinates are quantities of
atoms of the different elements C,H,O,N.
Find a basis
and dimension of the vector space V spanned by the vectors representing
the molecules of the ingredients in (a).
3.
Which of the following sets are vector subspaces of 
?
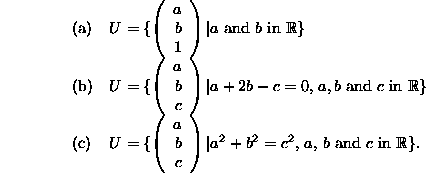
4.
(a) Is the set
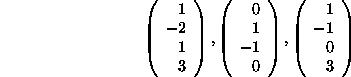
linearly independent in ?
(b) Is the set 
linearly independent in the
vector space of all functions 
?
5.
Prove that the set of all matrices is a vector space where
addition is addition of matrices, and scalar multiplication by
is given by multiplying every entry of a matrix
by 
.