Igor Kriz
Regular problems:
1.
Find the base change matrix from the basis
to the basis
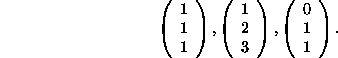
[Use the definition.]
2.
Recall that 
denotes the vector space of polynomials of
degrees 
. Prove that the derivative is a linear map
. Find the matrix of this map with respect
to the basis 
in the source and the same
basis in the target.
3.
Prove that the identity 
is a homeomorphism of metric spaces
where the metric is the Euclidean metric in the source and
the Postman metric 
in the target.
4.
Find a basis of the subspace of 
consisting of all
such that
[It is a null space.]
Challenge problems:
5.
By 
we denote the vector space of all 
matrices (row vectors). Now let A be an 
matrix.
The row space of A is the subspace of
spanned by the rows of A. Prove that the dimension of the column
space of A (called the column rank) is equal to the dimension
of the row space of A (called the row rank).
[We already know that equivalent row operations preserve the dimension
of the column space. Show that equivalent row operations actually
preserve the row space. Thus, it suffices to verify the statement for
matrices in reduced row echelon form.]
6.
Prove that a map of metric spaces 
is continuous if
and only if for every open subset 
, 
is open
in X
( is open if for every 
, there exists an 
such that 
).