Igor Kriz
Regular problems:
1.
Consider the function 
given by 
. Suppose 
is an inverse function to f, which is defined and has total differential
on an open set 
. Find the total differential of
g at the point 
.
2.
Find all the partial derivatives of the function 
up to order 3.
3.
Find the tangent plane to the surface in 
given
in parametric form by
at the point s=2, t=3.
4.
Let 
and
be two functions given by:
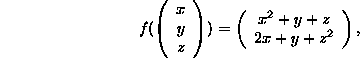
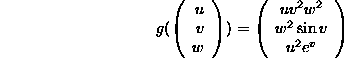
Compute Df, Dg, 
, 
.
Challenge problems:
5.
If f(0,0)=0 and
prove that the partial derivatives of f exist at every point of
, although f is not continuous at (0,0).
6.
Suppose 
where U is an open set in
. Prove that if all partial derivatives exist and
are bounded in U (i.e. all
their values are in an interval (-M,M) for some
constant M;SPMgt;0), then f is continuous.
[Hint: We proved in 295 that if 
is a one-variable function
in an interval satisfying 
everywhere, then
|f(x)-f(y)|;SPMlt;M|x-y|. Use this fact.]