More Coxeter Planes
The symmetry group of a regular polytope is a finite Coxeter
group, so all such polytopes have canonical projections into their
Coxeter planes. Collected here are
the 1-skeletons (wire frames) of the most interesting 4-dimensional
regular polytopes.
The 24-cell
[Download a
high-resolution version in Encapsulated PostScript]:
The symmetry group here is W(F4), and the polytope may
be constructed as the convex hull of the short (or long)
roots of an F4 root system. In fact, these are the roots
of a D4 root system, and as such they also have a
natural projection into a D4 Coxeter plane, but the
F4 projection has more symmetries.
The 24-cell has 24 vertices, 96 edges, 96 triangles and 24 octahedra.

The 600-cell
[Download a
high-resolution version in Encapsulated PostScript]:
The symmetry group here is W(H4), and the polytope may
be constructed as the convex hull of the H4 root system.
It has 120 vertices, 720 edges, 1200 triangles, and 600 tetrahedra.
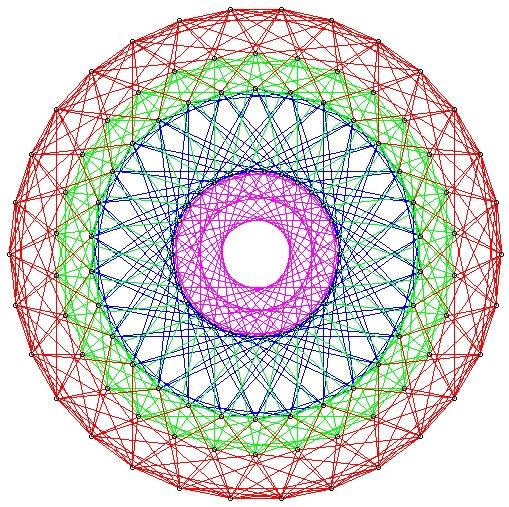
The 120-cell
[Download a
high-resolution version in Encapsulated PostScript]:
This is the dual of the 600-cell; it has 600 vertices, 1200 edges,
720 pentagons, and 120 dodecahedra.
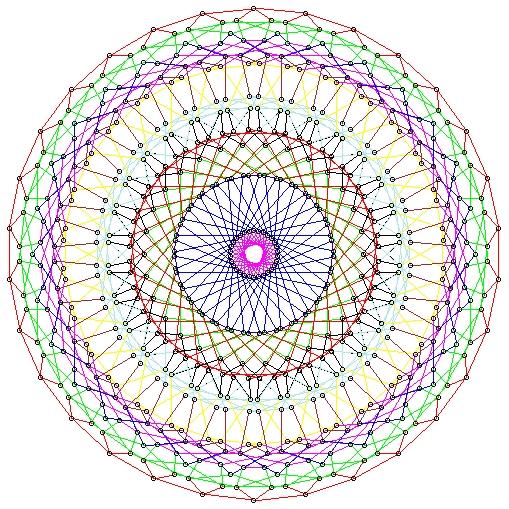
Back to John Stembridge's Home Page
or his
Archive of Research Data And Other Useful Stuff
or his main page on Coxeter Planes
This page last modified
Sun Dec 16 16:39:12 EST 2007



