http://www.math.uwaterloo.ca/navigation/ideas/grains/pythagoras.shtml
The Pythagorean Theorem says that if a right triangle has side lengths a, b, c (c=length of hypotenuse), then
a^2 + b^2 = c^2.
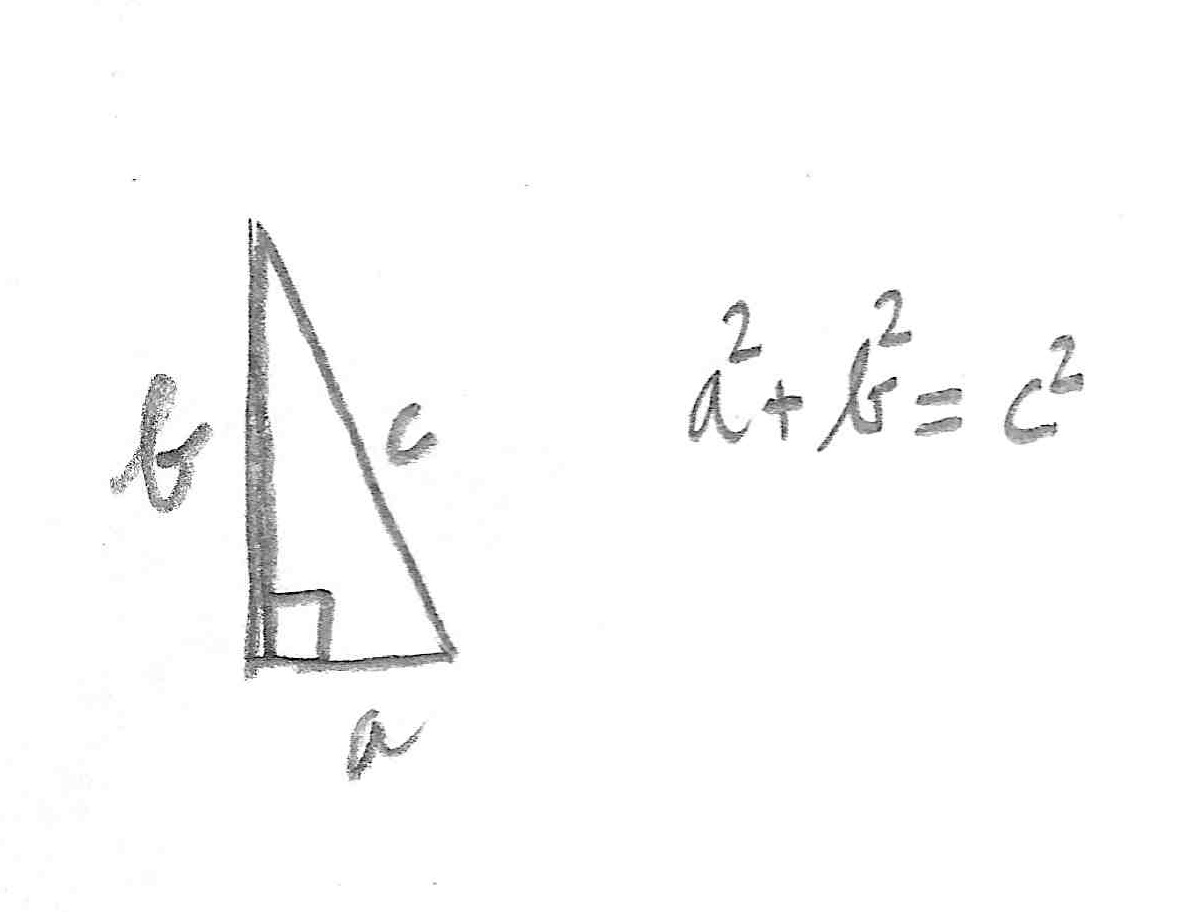
These sites give pictorial explanations of why this is true. The logic is based on the rules that the area of a rectangle is the product of the base times height and the area of a triangle is the half the product of the base times height
http://en.wikipedia.org/wiki/Platonic_solid
http://mathworld.wolfram.com/PlatonicSolid.html
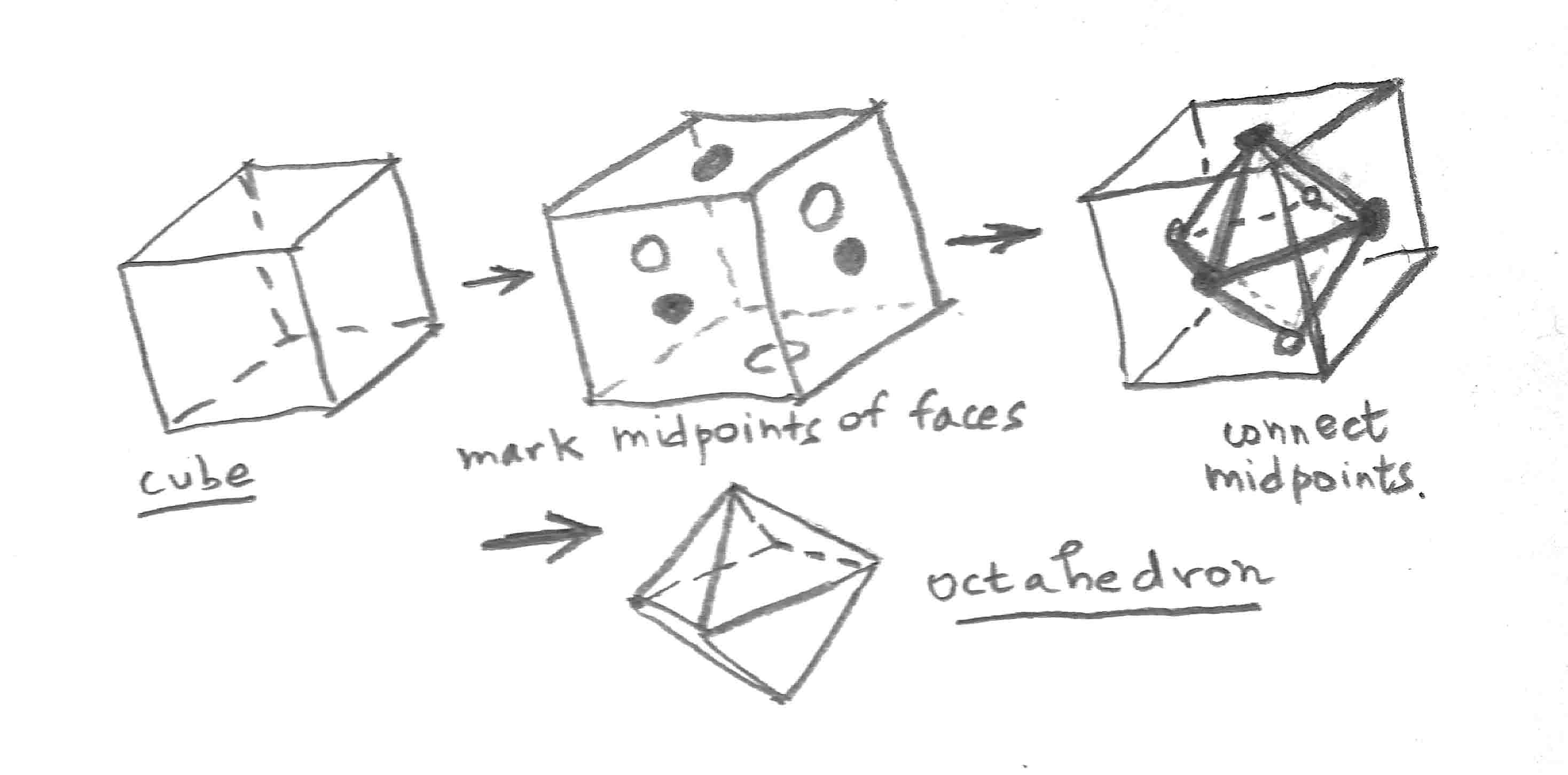
The five Platonic solids are the only solid figures defined by faces which are regular polygons. There are interesting ways to fit one of these into another.
http://www.youtube.com/user/Vihart#p/u/7/e4MSN6IImpI
http://www.nytimes.com/2011/01/18/science/18prof.html?ref=science
The Sierpinski triangle (mentioned by some math doodlers). There are videos of this on youtube.com.
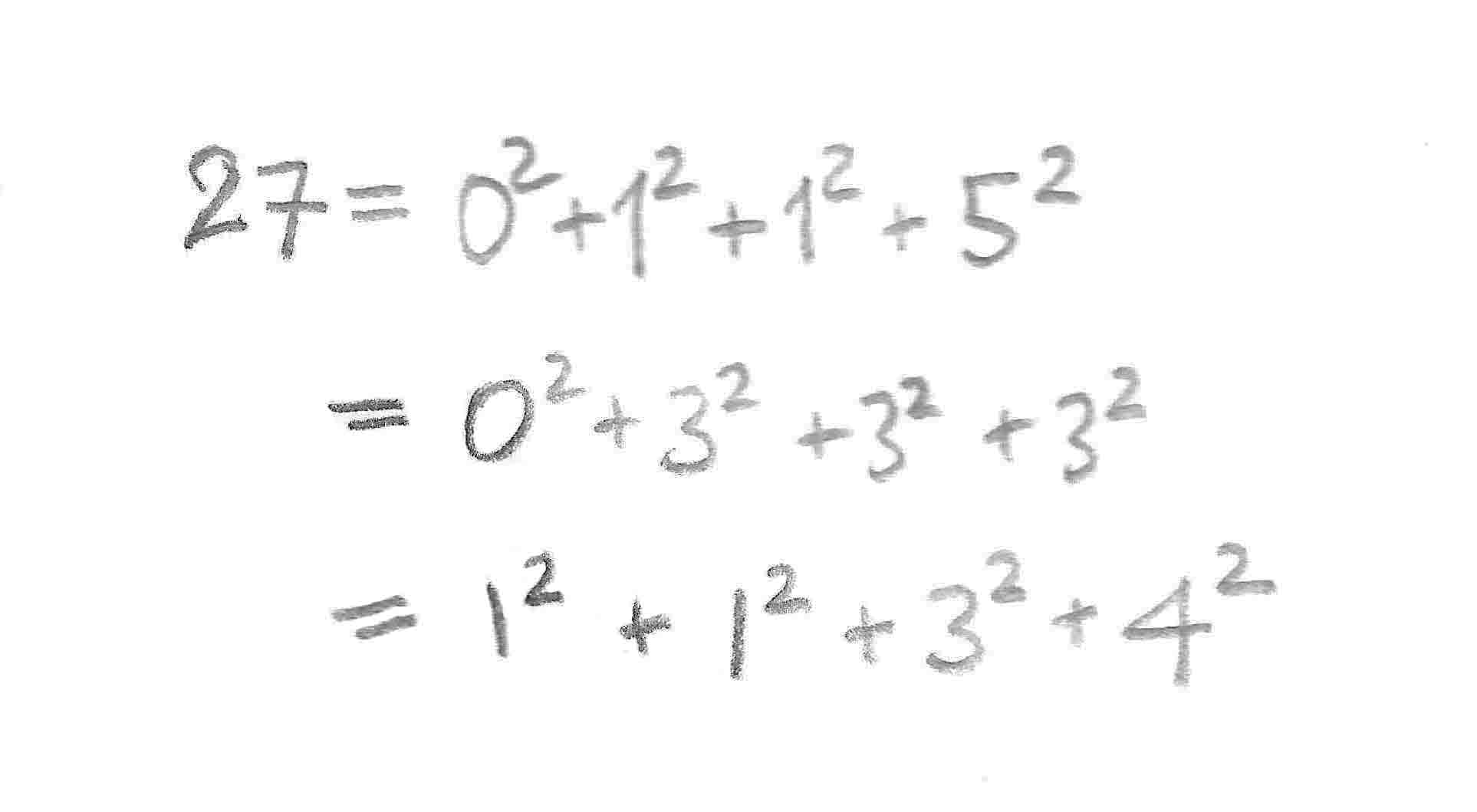
http://www.math.hmc.edu/funfacts/ffiles/20005.5.shtml
http://2000clicks.com/MathHelp/NumberSquareSums.aspx
A few things about sums of squares. The variables below represent integers. The meaning of a^n is a to the power n.
----------------
Suppose that a, b, c, d are integers. A product of sums of two squares (a^2+b^2)(c^2+d^2) is also a sum of two squares! There are integers e, f so that
(a^2+b^2)(c^2+d^2) = e^2+f^2.
----------------
Every positive integer is a sum of four squares. That is, given an integer n > 0, there are integers a, b, c, d so that
n=a^2+b^2+c^2+d^2.
For example, 5=1^2+2^2+0^2+0^2, 7=1^2+1^2+1^2+2^2.
Warning: an integer n may be a sum of four squares in many different ways. Try n=4 and n=12. Counting the number of different ways is a big deal.
In a map, the countries should have different colors if they share a common border. The Four Color Theorem says that you can color any map this way using only four colors. Try drawing a few maps to see if you can do it. (If two countries touch each other only at a point, you can ignore the different color requirement. )
The four color theorem is hard to prove. The first proof required computers.
There is a four-color game, played on a big piece of paper. Anna draws a country. Bill colors it then draws another country. Anna colors that and draws another country, and so on. A player loses if he or she makes two countries the same color in case they have a common border, or if he or she uses a fifth color.
http://en.wikipedia.org/wiki/M%C3%B6bius_strip
http://scidiv.bellevuecollege.edu/Math/Mobius.html
http://www.youtube.com/watch?v=rYIyXPnWPXc&feature=related
(this is an animation of a small person running around a möbius strip)
http://en.wikipedia.org/wiki/Klein_bottle
http://www.youtube.com/watch?v=E8rifKlq5hc (a nice video)
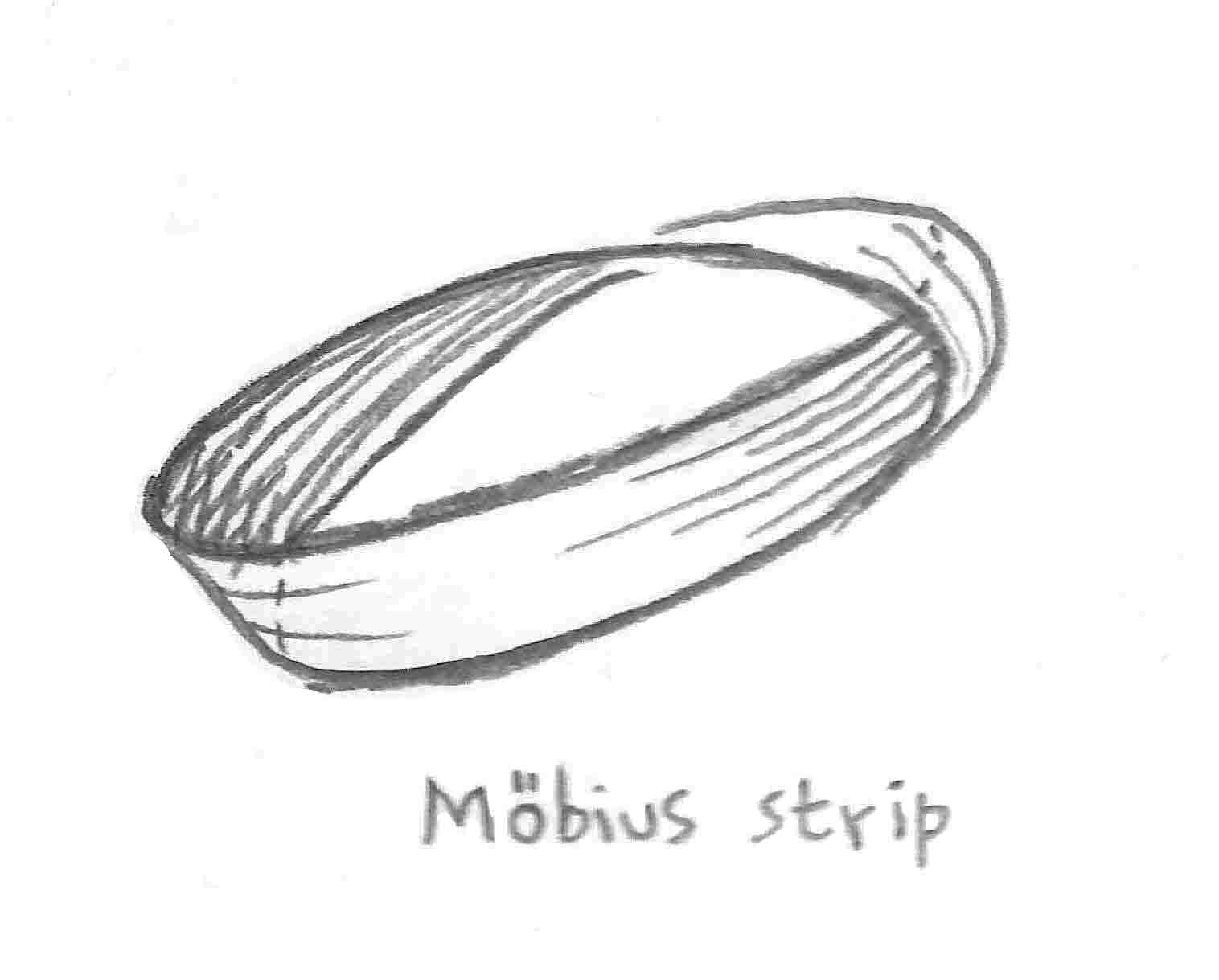
Möbius strip (also: Moebius strip, Möbius band).
This is a surface which, remarkably, has only one side and one edge. You can make one with paper, scissors and glue or tape.
It is related to the Klein bottle, which has just one side (so inside = outside!).