Math 215 Section 40 - Winter 99
Quiz # 5: SOLUTIONS
Problem 1. A metal plate occupies the triangular region with vertices at (0,0), (0,1) and (1,0). The temperature of the plate at the point (x,y) is given by the function T(x,y) = x(1-x-y).
(a) Find the critical points of the function T.
Solution:
is the zero vector iff -x=0 and
1-2x-y=0, that is iff x=0 and y=1. So this function
has exactly one critical point: (0,1).
(b) Find the hottest point on the plate. PLEASE EXPLAIN YOUR METHOD.
Solution: By part (a) the function T does not have any critical points in the interior of the region. Therefore, the function attains its maximum over the region at a boundary point. The region's boundary consists of three line segments, namely:
where (III) is the hypotenuse of the triangle and we have used the equation of the line through (0,1) and (1,0). It's immediate that the function T is zero at every point of sides (I) and (III). On side (II), it agrees with the function of x
We are to find the absolute maximum of this function in the range 
.
One variable methods show that the maximum of f is attained at 
.
Since 
is greater than zero (the value of
T on sides (I) and (III)), the point 
is the hottest point
on the plate. By the way, the temperature there is 
units.
Problem 2. Using the method of Lagrange multipliers, find the
point on the ellipsoid
where the
function h(x,y,z) = x+2y+z is maximal.
Solution: The ellipsoid is a level surface of the function
. Therefore,
we have to solve the system of equations: 
and g=1. Writing this as a system of scalar equations yields:
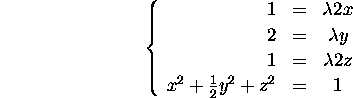
From the first three equations we can find x, y and z in terms of
:
Substituting back into the fourth equation (remember to use the constraint!) we get
which yields: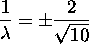 
.
Looking at the expressions for x, y and z in terms of and the
formula for h, it is clear that the maximum is obtained at the point with
, so the final answer is:
