
First let's think about the slice. We visualize this below:

then we need to go to step 2:
We want to find the volume of each slice (shown above). The volume will be the length times width times height. The height is just "dy", the length is just "L", and the width isn't so obvious. Let's look at the tube end-on to see what the width is:
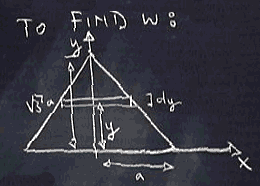
The first thing we need to do is find the equation of the line that gives the hypotenuse of right side the triangle. We know the y-intercept is sqrt(3)a (the height of the triangle) and we can find the slope of the line using rise over run. The slope is thus simply -(sqrt(3) a)/a = -sqrt(3). Therefore, the equation of the line is:
We then need to solve this equation for x so that we can integrate in terms of dy, not x. By solving for x we get:
We know that w is 2x because we have only found x for half of the triangle. Now we need to multipy by 2 so w = 2a - (2/sqrt(3))y.
The volume of the slice is then length times width times height, or
To find the volume, we integrate the formula above from 0 to sqrt(3)a. Using our simple integrating process, we find the volume of the figure to be L(sqrt(3))a^2, which looks quite similar to the answer we got by using vertical slices.