Mass and Work
Now that we have found the volume of the object, we need to
now find the mass and work of the object.
Mass

To figure the mass, we must slice the object vertically because
the density changes as we move along the z axis. We
know the mass of a slice is (volume)(density). We know the volume of
the slice is sqrt(3)(a^2)dz, so for each slice
(volume)(density) = sqrt(3)(a^2)dz * (2+z)
We simply integrate this function from 0 to L, which is quite
easy, and this will give us the mass of the object.
Work
Finally, suppose that this is a tank of water and we want to find the
work to pump all of the water out the top. Because the work changes
depending on our y coordinate (see the figure below), we
have to slice horizontally. Let's use the figure for the horizontally
sliced volume calculation to see how to do this.
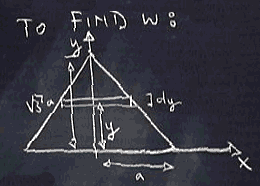 We know that work is (force)(distance), and that force = weight. If
this is a tank of water, we know that the density of water is
62.4 lbs/ft3; let's assume that
the other dimensions of the tank are in feet for convenience. Then
the force is (density)(volume), or
weight of slice = (density)(volume) = (62.4)(L ((2a - 2/sqrt(3)) y) (dy)).
(We got the volume from the horizontal
volume slice calculation). Then the distance each 'slice' of
water needs to be lifted is
distance for slice = sqrt(3) a - y,
so the work to lift the one slice of water is
(force)(distance) = (62.4)(L ((2a - 2/sqrt(3)) y) (dy)) * (sqrt(3) a - y).
To find the full volume, we have to integrate this for y between 0 and
sqrt(3)a.
We know that work is (force)(distance), and that force = weight. If
this is a tank of water, we know that the density of water is
62.4 lbs/ft3; let's assume that
the other dimensions of the tank are in feet for convenience. Then
the force is (density)(volume), or
weight of slice = (density)(volume) = (62.4)(L ((2a - 2/sqrt(3)) y) (dy)).
(We got the volume from the horizontal
volume slice calculation). Then the distance each 'slice' of
water needs to be lifted is
distance for slice = sqrt(3) a - y,
so the work to lift the one slice of water is
(force)(distance) = (62.4)(L ((2a - 2/sqrt(3)) y) (dy)) * (sqrt(3) a - y).
To find the full volume, we have to integrate this for y between 0 and
sqrt(3)a.
Back to the Outline
Next


