>	with(plottools): with(plots): with(linalg):

 

Let's look at the vector function 

>	r := t -> [2*cos(3*t), t^2, 2*t];

 

(1)

 

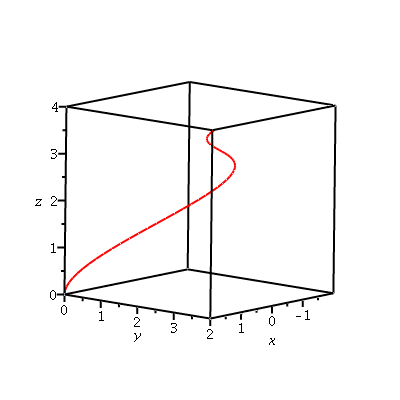
This describes the space curve 

>	sc := spacecurve(r(t), t=0..2,color=red,thickness=2,axes=boxed,labels=[x,y,z],scaling=constrained): sc;

 

The derivative is a tangent vector to this 

>	rp := s -> eval(diff(r(t),t),{t=s}):

 

and the unit tangentn is this normalized 

>	ut := u -> eval(normalize(rp(t)),{t=u}):

 

This is tangent to any point on r, and its derivative gives the primary normal to the curve: 

>	utp := v -> eval(map(diff,ut(t),t),{t=v}): un := w -> eval(normalize(utp(t)),{t=w}):

 

>	tplot := i -> display3d(sc,arrow(r(i*.05),ut(i*.05),thickness=3,color=blue),arrow(r(i*.05),un(i*.05),thickness=3,color="Magenta")):

 

>	display3d([sc, seq(tplot(i),i=1..40)],insequence=true,scaling=constrained);

 

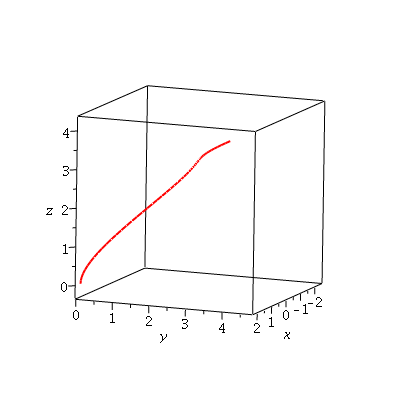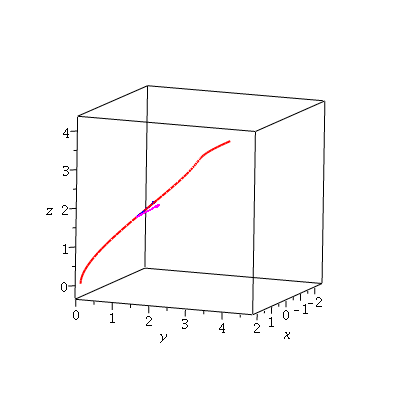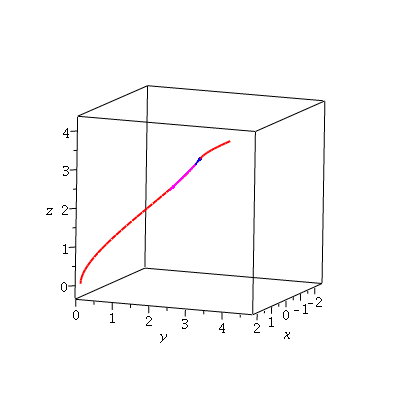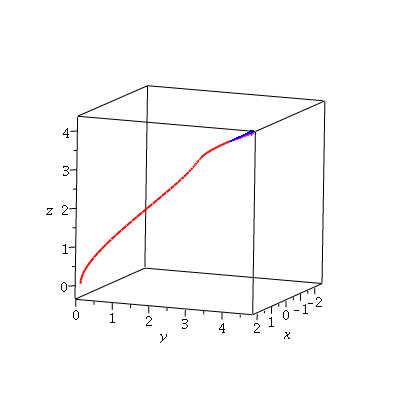
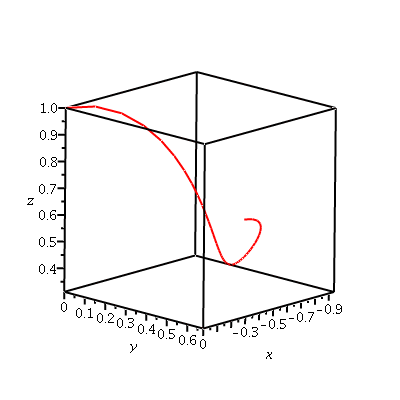
The unit tangent, however, also defines a space curve, if we think of it as a position vector pointing from the origin to the point ut(t): 

>	usc := spacecurve(ut(t),t=0..1,axes=boxed,color=red,thickness=2,labels=[x,y,z]): usc;

 

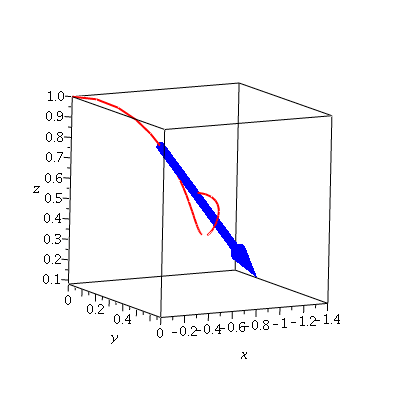
We know that the derivative of this vector function is the tangent to this curve: ut'(t) is tangent to the spacecurve given by ut(t).  And we know that ut'(t) is perpendicular to the original.  for example, at t=0.1, 

>	display3d(usc, arrow(ut(.1),un(.1),color=blue));