Igor Kriz
Regular problems:
1.
Let
(a) Find a basis of Null(A).
(b) Find a basis of Col(A).
2.
Review problem:
Find the shortest distance from a given point (0,b) on the y-axis to the
parabola 
. [Express the distance as a function, and find its
minimum using derivatives.]
3.
Let V be a vector space, let S and T be two subsets of V (not necessarily subspaces).
(a) Prove that 
.
(b) Find an example where 
4. Consider the set
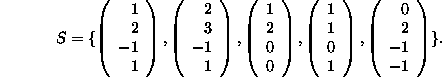
Does S span 
? Is S linearly independent in ?
Challenge problems:
5.
Linear recursions continued: Suppose a sequence 
is defined as
follows:
,..., 
are given, and
(a) Suppose that the polynomial
has a root 
of multiplicity 
(i.e. 
divides p(x)). Show that then the sequences
for i;SPMlt;k-1 and all their linear combinations satisfy the relation (1). [Hint: use derivatives.]
(b) Using (a), solve the following problem: Suppose numbers 
are given as follows: 
, 
, 
for 
. Find a formula for .
(c) Consider the sequence 1,4,2,1,4,2,1,4,2,.... Thus,
, 
and 
for all natural numbers n. Find a formula for which uses only
arithmetic operations (addition, multiplication, subtraction, division,
taking powers and roots). [Write the
sequence in terms of a linear recursion. This does
not use (a) or (b), but it uses complex numbers.]
6.
Review problem: If
where 
are real constants, prove that the equation
has at least one real solution 
.
