Igor Kriz
Regular problems:
1.
Find the partial derivatives of the function 
given by 
where
is the open set of all
such that
x;SPMgt;0, y;SPMgt;0,z;SPMgt;0.
2.
At what points 
are the following functions continuous? (Prove using theorems from class.)
(a) 
(b) 
.
3.
Let
Show that 
is continuous
at 
, but that
4.
(a) Prove that an intersection of subspaces of a vector space U is a subspace.
(b) Find a basis of the intersection of the subspaces of 
spanned by
and
.
[Express the problem as a system of linear equations.]
Challenge problems:
5.
In a metric space X, prove that: (a) An intersection of two open sets is open.
(b) A union of arbitrarily (possibly infinitely) many open sets is open.
(c) A set is open if and only it is a union of (possibly infinitely many)
open balls (sets of the form
).
6.
In special relativity theory,
particles are represented by points in timespace 
where x,y,z
are cartesian coordiantes in space, t is time. An
inertial observer travels at constant speed in space (possibly
0, but that is relative). Einstein's basic principle says that
all laws of physics are equal for all inertial observers. In
particular, the speed of light is the same: 
.
The spacetime coordinate system of one inertial observer A is
related to the coordinate system 
of another inertial observer B
by a Lorentz transformation, which is a linear transformation
satisfying
If B travels at speed v along the x axis relative to A, then the Lorentz transformation is
where
is called the Lorentz factor.
(a) Verify that the Lorentz transformation defined above satisfies (1).
(b) Considering v,c constants (which they are), the Lorentz transformation
is a linear map 
. Find
its matrix (with respect to standard bases).
(c) Using symmetry, find the Lorentz transformation in the general case when B
travels in space at constant vector speed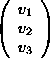 
relative to A.
(d) A space station A carries a gyroscopic device which specifies
Cartesian coordinates in space with origin A. At time 0, a rocket B
departs from A at constant speed
in the direction of the x coordinate.
The rocket also
carries a gyroscope which allows it to maintain a coordinate
system parallel to that of A. Now an explosion occurs at time
in coordinates
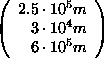relative to the space station A. At what time, and with what
coordinates will the explosion occur relative to B? [Use a calculator.]
