Index
- Data analysis.
- Constructing linear models from real-world data sets.
- Functions.
- A basic "toolkit": constant, linear, quadratic, cubic, square root, absolute
value, reciprocal, sine functions.
- Transformations, combinations, inverses, polynomial, rational, exponential,
logarithmic.
- Re-expression to linearize data for analysis.
- Large-scale modeling (including applications of basic probability).
- Trigonometry: unit-circle, functional approach.
- Triangle applications done last.
- Basic principles: the same as for our reformed calculus.
- The rule of four. Every topic should be studied geometrically,
numerically, and algebraically, and communicated back to the instructor in a literate
fashion.
- The way of Archimedes. Formal definitions and procedures evolve from the
investigation of practical problems.
- Reformed text used: Contemporary Precalculus through Applications, by the
mathematics faculty of the North Carolina School of Science and Mathematics, Janson,
1992.
- Less emphasis on manual algebraic manipulation, more on concepts.
- Emphasis on cooperative learning, in-class and with homework groups; de-emphasis
on lecturing.
- Both individual and group.
- Individual: typically 4-5 exercises daily, but nonrepetitive and nontrivial.
- Group: typically 3-4 exercises once or twice per week.
- Emphasis on applications and concepts.
- Writing skills and clarity of exposition stressed.
The following table represents the measured amount g, in grams, of a certain
chemical compound that can be dissolved in one liter of water at various
temperatures T, measured in degrees Celsius.
T 10 20 30 40 50 60 70 80 90
g 1.70 1.23 0.86 0.65 0.47 0.34 0.25 0.18 0.13
- In this relationship, which variable would it be natural to view as the
independent variable and which as the dependent variable? Explain. (An aside: In
practice, we would probably not add the command to "Explain." The students learn
early in the course that this is a natural part of answering a question such as
this.)
- Using median-median line regression, find a linear expression that models the
number of grams of solute as a function of the temperature of the water.
- Describe the real-world physical meaning of the slope of the line given by your
linear model.
- Describe the real-world physical meaning of each of the axis intercepts of the
line given by your linear model.
- What are the natural domain and range of the function defining your linear model,
taking into account physical constraints?
- Find an exponential model for the number of grams of solute as a function of the
temperature of the water.
- Why would you expect the sign of the exponent in the equation that defines this
model to be as it is?
- Let the above data set be called Data Set A. Suppose that another experimenter
performs the same experiment and obtains other figures that will be called Data Set B.
For low temperatures, the figures of Data Set B show that more of the compound can be
dissolved in a liter of water than do the figures of Data Set A, but for high
temperatures the opposite is true. If Data Set B were to be used instead of Data Set
A to construct the exponential model, what would be the likely effect on each of the
numbers appearing in the equation that defines the model?
- Which of the two models do you believe is better?
- The text assumes technology is available to facilitate computations and graphing;
the numbers and functions used are not always "nice," often arising from real-world
data.
- TI-82 calculators are
(essentially) required of all students; a few use other calculators at their own risk.
- Portable.
- Easy to learn to use.
- Have built-in features especially for the text being used.
- Programs can be transferred by cable link directly into calculators.
- The use of technology allows the exploration of topics once inaccessible in
precalculus.
- For instance, students can learn to set up optimization problems, then find the
solutions using the calculator. When they get to optimization problems in calculus,
they already understand the concept and only have to learn the new methods. (Also,
the graphical insight they get from solving the problems with the calculator can make
them more alert to the need for knowing whether a place where a derivative is zero is
a local maximum, a local minimum, or neither. In short, they may be less likely
merely to set a derivative equal to zero and declare the problem finished.) An
example follows.
Find the volume of the largest open box that can be formed from an 18.4" by
24.2" rectangle of cardboard by cutting congruent squares from each corner and folding
up the flaps.
The students will find that
V(x)=x(18.4-2x)(24.2-2x),
where x is the side of each square and V(x) is the corresponding box volume. (Of
course, finding this formula is the hard part of the exercise.) To finish solving
using the calculator, they will also find it useful to know that the natural domain
for this function is the closed interval [0,9.2]. Some experimenting (or some
estimating of the size of the function) shows that the natural range will fit in the
closed interval [0,1000]. Those familiar with the TI-82 will now recognize the
following as the resulting graph window settings screen and the output from the
calculator's graphical optimization routine.
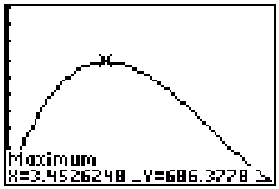
The maximum volume is therefore about 686 cubic inches.
- We assume that the students have already seen, though not necessarily totally
mastered, such topics as:
- The distance formula; laws of exponents and radicals; factoring of polynomials;
simplification of rational algebraic expressions; equations of straight lines.
- Solution of equations, including those involving rational expressions and systems
of linear equations; solution of inequalities, including absolute-value inequalities.
- Elementary properties of functions and graphs.
- Knowledge of trigonometry is not assumed; however, most students have some.
- Have our students really seen this material before? In most cases, they have.
Here is the distribution of students in Math 105 in the fall, 1993 semester by the
number of years of high school or college mathematics taken previously.
- 1 year: 0.7%
- 2 years: 1.4%
- 3 years: 15.9%
- 4 years: 77.5%
- 5 or more years: 4.3%
- Though the students have seen the material mentioned above, most have not mastered
it, and are in Math 105 precisely because they failed a calculus placement test over
these skills or by self-placement due to lack of comfort with the material.
- Problem: Since our precalculus course does not stress
manipulative algebraic skills, how can we guarantee that the students have these
skills before being passed on to calculus?
- Solution: Gateway testing.
- Covers skills, not concepts.
- Comprehensive and rigorous.
- Pass/fail grading, but high score needed to pass.
- Usually offered outside class.
- May be repeatedly retried without penalty as long as it is eventually passed.
- New version of test available for each attempt.
- If a student is not at the skill level needed to pass the test, it is
primarily the student's responsibility to reach that level, not the instructor's to
spend valuable class time filling in holes in the students' knowledge that will vary
from student to student.
- See the following article for more on our gateway testing program.
We also have a WWW document available describing the UM gateway
testing program, and another document describing the Lotus 123/TeX-based gateway testing software mentioned in the above article. This
last-mentioned document includes a button you can push to have this software delivered
into your disk directory.
- 3-4 students per group.
- Formed by instructors, not self-selected by students.
- Changed every 3-4 weeks.
- One or two group homework sets per week.
- Group homework is held to high standards of completeness, accuracy, and literacy.
- Group member roles (which change for each homework set).
- Recorder: keeps the "minutes".
- Scribe: writes up the final version of the homework.
- Clarifier: verbally summarizes and clarifies discussions during
the group meetings.
- Manager: gets the group together, often provides refreshments.
- Students work on activities in pairs or larger groups, usually not the
same groups as the homework groups.
- Activities are carefully chosen to get the students to interact, test out ideas on
each other, reinforce individual understanding.
- Instructor has many roles, but not primarily that of a lecturer.
- Watch for general points of confusion; be prepared to interrupt and clarify.
- Summarize when groups are generally reaching some conclusion.
- Re-engage students not actively engaged with their group.
- One-week training session (or professional
development program) for those teaching our reformed precalculus or calculus for
the first time.
- What to do when you have de-emphasized lecturing.
- Emphasis on concepts over manipulations.
- In-class cooperative learning.
- Homework groups.
- "Sick" groups and other problems with groups.
- The proper use of technology.
- Weekly meetings with instructors during the semester.
- Students learn concepts better.
- Students have skills reinforced within the context of new material (so there is
far less boredom).
- Students recognize applications as realistic and relevant.
- Technology allows realistic numbers and more complicated computations.
- Socialization valuable - mathematics not presented as "loner" activity.
- Emphasis on writing and other communication skills.
- More work (and initially more stressful) for instructor.
- Requires instructor training.
- More difficult to implement with large class sizes.
- Technology absolutely required.
- More expensive for students.
- "Culture shock" for students - "I've never had a math course like this before.
Will this really prepare me for calculus?"
Return to the top of this document
Go back to General
Information on UM Precalculus
Go back to Traditional UM
Precalculus
Last modified Fri 12 May 1995 12:19 EDT
Bob Megginson
Department of Mathematics
University of Michigan
meggin@math.lsa.umich.edu