The N-Soliton of the Focusing Nonlinear Schrödinger Equation for N Large
G. D. Lyng and P. D. Miller
Department of Mathematics, University of Michigan, Ann Arbor
Abstract:
We present a detailed analysis of the solution of the focusing nonlinear Schrödinger equation with initial condition ψ(x,0)=Nsech(x) in the limit N→∞. We begin by presenting new and more accurate numerical reconstructions of the N-soliton by inverse scattering (numerical linear algebra) for N=5, 10, 20, and 40. We then recast the inverse-scattering problem as a Riemann-Hilbert problem and provide a rigorous asymptotic analysis of this problem in the large-N limit. For those (x,t) where results have been obtained by other authors, we improve the error estimates from O(N-1/3) to O(N-1). We also analyze the Fourier power spectrum in this regime and relate the results to the optical phenomenon of supercontinuum generation. We then study the N-soliton for values of (x,t) where analysis has not been carried out before, and we uncover new phenomena. The main discovery of this paper is the mathematical mechanism for a secondary caustic (phase transition), which turns out to differ from the mechanism that generates the primary caustic. The mechanism for the generation of the secondary caustic depends essentially on the discrete nature of the spectrum of the N-soliton. Moreover, these results evidently cannot be recovered from an analysis of an ostensibly similar "condensed-pole" Riemann-Hilbert problem.
Mechanism Behind the Secondary Caustic: the Movie
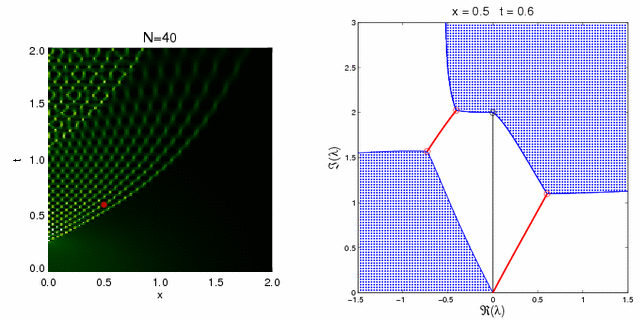
Just click on the image to begin the movie!