Site menu:

Latest news:

Aug 6, 2022:
New references have been added to the research descriptions below.

Go to current research »

Information:

Looking for more materials? Try looking under Teaching (lecture notes) or Publications (reprints).

Note: codes in square brackets on this page refer to entries in the publication list. Click to see the complete reference.

Jump to:

Search box:


on this site:
on the web:

Research

Current Topics of Research

Here are some of the topics of current research interest.

  1. Universality in Nonlinear Waves

    Certain features of solutions of nonlinear wave equations can be independent of initial conditions or even the details of the equation. This is a nonlinear-wave analogue of universality in mathematical physics.

    This work is represented in publications [J65], [J66], and [J68].

  2. Rogue Waves and Related Solutions of Nonlinear Wave Equations

    This topic concerns mathematical models for large-amplitude disturbances that appear with little if any warning on a background wave. Such waves have been the focus of intense study because they can cause structural damage to ships, drilling platforms, and coastal zones. Prof. Miller has been working on putting rogue-wave type solutions of wave equations on a more analytic background so that they can be studied in various asymptotic limits with relative ease.

    This work is represented in publications [J59], [J64], [J67] and [J68].

  3. Semiclassical Asymptotics for Nonlinear Waves

    Prof. Miller has been studying the behavior of solutions of nonlinear wave equations that may be characterized as having features on two disparate scales in both space and time. A typical situation is that a problem is posed with initial data having some fixed spatial scale while the wave equation being solved favors oscillations of a relatively short wavelength. Such situations are frequently called "semiclassical" since a prototypical example arises from Schrödinger's equation of quantum mechanics with macroscopically-scaled initial data in the nearly classical situation when Planck's constant is small.

    There is a great advantage in studying semiclassical behavior in the context of nonlinear wave equations that are completely integrable by an inverse-scattering transform because in principle all details of the relevant asymptotic limits can be worked out exactly. However, in some cases (the focusing cubic nonlinear Schrödinger equation is an example) it is not even clear whether a semiclassical limit exists in any reasonable sense because one is led by formal reasoning to consider a limiting process that is not even a well-posed initial-value problem. Equations like this call for great scrutiny and careful mathematical analysis, and this is the subject of much of Prof. Miller's ongoing work.

    The plot in the banner of this website shows typical dynamics in space (horizontal) and time (vertical) of a solution to the focusing nonlinear Schrödinger equation in the semiclassical regime. For more information about this image, see [J18] and [J31], and to see other images of this type corresponding to different solutions, see [J27]. The plot in the paragraph above shows the dynamics of a solution in the semiclassical regime of the sine-Gordon equation. This equation has the additional complication of "topological charge", which leads to new phenomena in the semiclassical limit; see [J35].

    This work is represented in publications [J18], [J27], [J28], [J31], [J34], [J35], [J37], [J38], [J39], [J40], [J41], [J42], [J47], [J50], [J51], [J53], [J55], and [J60], as well as in the monograph [M1].

  4. Random Matrix Theory and Generalizations

    The truly remarkable coincidences between the statistics of sets of data arising in various types of experiments and the statistics of the eigenvalues of large random matrices have inspired a recent interest throughout the mathematical community in the "classical" subject of random matrix theory. Indeed, data ranging from the practical (bus arrival times in Cuernavaca, Mexico) to the abstract (spacings of zeros of the Riemann zeta function on the critical line) have been shown to agree well with statistical laws that govern the spectra of random matrices. Whether these coincidences are just so, or whether there is some reason for this agreement, is not clear in general.

    From the mathematical side, many interesting questions revolve around the subject of studying random processes that can be analyzed in great detail, and establishing what kind of statistical laws emerge in the "scaling limit" (this is the limit in which the size of the matrix goes to infinity in the case of random matrix theory). Every time such a calculation leads to the conclusion that a system is governed by the laws of random matrix theory, a point is scored for "universality". Universality of random matrix theory is an analogue for dependent random variables of the central limit theorem for independent random variables. Limit laws obtained from random matrix theory are definitely non-Gaussian.

    Prof. Miller's work on this subject is related to establishing universality of random matrix theory statistics in various problems. With J. Baik, T. Kriecherbauer, and K. McLaughlin, he has studied the problem of random tilings of hexagons by rhombus tiles (see the figure in the paragraph above for an example) and shown that universality holds both in the bulk (the so-called "temperate region" where the tiles are randomly arranged) and also at the edge (the boundary between the temperate region and the so-called "polar zones" where the tiles are all oriented the same way), but with different limit laws connected with random matrix theory. Working with J. Baik, P. Deift, K. McLaughlin, and X. Zhou, he has also shown universality in a problem of percolation (transport in random media). His current interests lie in developing mathematical methods to extend the validity of universality beyond the classes of probability measures usually considered for random matrices, in particular to admit "nonanalytic weights".

    This work is represented in publications [J26], [J29], and [J36], and in the monograph [M2].

  5. Nonselfadjoint Eigenvalue Problems

    Another aspect of Prof. Miller's ongoing work concerns eigenvalue problems for operators that are not self-adjoint, or more generally linear spectral problems that cannot be easily formulated in terms of the spectrum of a given operator at all. These kinds of problems arise in the framework of the scattering and inverse-scattering transforms for solving certain integrable problems of nonlinear wave theory. For example, to calculate the image of the initial data for the focusing nonlinear Schrödinger equation in the scattering transform domain, one must analyze the eigenvalue problem for the nonselfadjoint Zakharov-Shabat operator.

    In practice, one needs to be able to extract quantitative information about the spectrum for problems like this. Generally this must be viewed as a difficult task, perhaps best left to scientific computation. But in many situations of interest, there is a small parameter in the spectral problem that can be exploited by casting the spectral problem as an asymptotic calculation. This is exactly what occurs in studying the scattering problems associated with integrable nonlinear wave equations in the semiclassical limit.

    This work is represented by the publications [J24], [J34], [J43], [J44], [J46], [J49], and [J52].

  6. Riemann-Hilbert Problems, Orthogonal Polynomials, Approximation Theory and Special Functions

    A common link between Prof. Miller's interests in nonlinear waves and in random matrix theory is that in both of these subjects the mathematical theory of Riemann-Hilbert problems plays an important role. A Riemann-Hilbert problem is a problem of complex analysis in which a piecewise-analytic unknown is to be reconstructed by certain discontinuity data given along contours in the complex plane. A central theme of Prof. Miller's current work is the generalization of various asymptotic methods for Riemann-Hilbert problems (in particular, the Deift-Zhou steepest descent technique) to contexts where the Riemann-Hilbert problem is "singular" in some sense. For example, the discontinuity contour may degenerate to a collection of point singularities, or the given discontinuity data may fail to be sufficiently smooth along the jump contour.

    One of the simplest Riemann-Hilbert problems is that which characterizes the system of orthogonal polynomials with a given measure of orthogonality on the real line, or on the unit circle. Not only is this Riemann-Hilbert problem simple to formulate, but also it is of far-reaching importance because of the role that orthogonal polynomials play in random matrix theory. Therefore, much of Prof. Miller's current interests involve the asymptotic characterization of orthogonal polynomials in the limit of large degree, in various circumstances where the measure of orthogonality is "defective" in some way. The image in the above paragraph shows one aspect of this asymptotic theory, the presence of a fixed finite number (6 in the figure, while the polynomial has degree 104) of "spurious zeros" of orthogonal polynomials on the unit circle when the weight function has a related number (7 in the example shown in the figure) of points of discontinuity of any derivative. For more information about this phenomenon, click here.

    Riemann-Hilbert problems also generalize well-known integral representations of classical special functions to the nonlinear regime, characterizing nonlinear special functions known as Painlevé transcendants that arise in many applications.

    This work is represented in publications [J29], [J30], [J32], [J33], [J36], [J45], [J48], [J56], [J57], [J61], [J62], [J64], [J66], [J69], and [J70], and in the monograph [M2].

Earlier Work

Prof. Miller's earlier work was influenced by his postdoctoral experience in an Optical Sciences department, and had a more applied flavor. Here is a list of some of the topics addressed by this earlier body of work.

  1. Optimal Design of Linear Waveguides

    The stationary propagation of low-intensity paraxial light rays through an inhomogenous planar medium is described by the 1+1 dimensional linear Schrödinger equation with a "time" dependent potential function (the time is really the spatial direction of beam propagation). In applications of integrated optics, one is faced with a problem of design of devices like multiple-core couplers, optical power dividers, and waveguide junctions. These devices should exhibit minimal scattering loss. The problem is to determine how the distribution of the refractive index in the slab (i.e. the potential function) should be specified to minimize the scattering losses and simultaneously satisfy design specifications for device performance. In a sequence of papers with N. N. Akhmediev of the Australian National University, Prof. Miller has shown that all of these integrated optical devices can be designed to specification and to have zero scattering loss. This is done by making a connection between the potential function and the self-induced nonlinear potential of an integrable vector nonlinear Schrödinger equation. Dark soliton potentials correspond to perfect twin-core couplers and to zero-crosstalk waveguide junction devices. Bright soliton potentials yield lossless power dividers. This work provides the general solution of the linear time-dependent Schrödinger equation for such nonlinear potentials, and in subsequent work (with J. Besley, M. Weinstein, and A. Soffer) Prof. Miller has used this theory to study periodic waveguides.

    In collaboration with a group of scientists in the Department of Theoretical Physics at the University of Sydney and the Optical Fibre Technology Centre, Prof. Miller has studied the way that some permanent refractive index distributions can form in a natural way in a planar medium that is photosensitive to ultraviolet light. A beam of UV incident on the medium initially diffracts, but ultimately changes the refractive index, leaving behind a "self-written" channel waveguide. This waveguide can then be used as a permanent device to guide light at a frequency to which the material is not photosensitive. This collaborative work investigates the self-similar solutions of the self-writing problem.

    This work is represented in publications [J6], [J7], [J13], [J14], [J15], [J16], [J20], and [J23].

  2. Nonlinear Fiber Optics

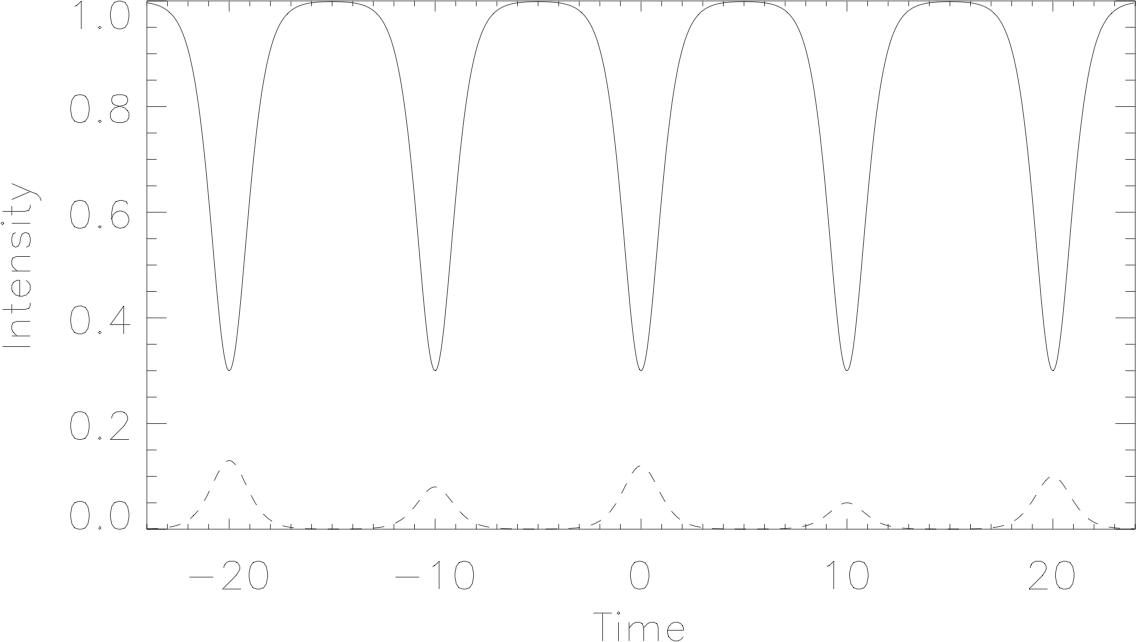    Along with N. N. Akhmediev and A. Ankiewicz of the Australian National University, Prof. Miller has proposed an all-optical data transmission system that operates in the regime of normal dispersion, in which the nonlinear response in glass fibers favors the so-called "dark soliton" pulses instead of "bright soliton" ones. To achieve terabit per second transmission rates it is essential to avoid slow electronic coding and decoding methods, and unfortunately using dark solitons as bits in a data stream seems to require electronics. The novel scheme proposed overcomes this limitation by allowing data encoded in low-intensity linear pulses to ride along a rigid train of dark nonlinear pulses like widgets on a conveyor belt. Because the soliton train is periodic, it can be generated without "smart" electronics. It has been shown that many such "optical conveyor belts" can share the same fiber without any signal distortion, in spite of the essential nonlinearity.

    This work is represented in publication [J10].

  3. Nonlinear Waveguide Arrays

    For several years it has been known that the effect of third order nonlinearity on twin-core optical couplers is to allow them to function as power controlled switches. Once such nonlinear couplers were understood, it was natural to consider the effect of having many cores, say arranged in a linear array with nearest neighbor coupling. It was found that power controlled switching became chaotic and thus hard to control as the number of cores was increased. While working in collaboration with Ole Bang at the Australian National University, Prof. Miller has proposed a new switching method in many-core arrays that is insensitive to the number of cores in the array. The method uses the stability of highly localized solutions of the discrete nonlinear Schrödinger equation that is the relevant model. All-optical switching is very important in the future of telecommunications.

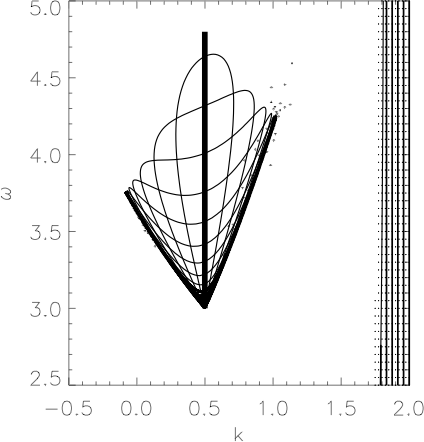    Prof. Miller has also studied excitations in the arrays that are not localized, but rather are extended over many cores of the array. The description of these excitations was carried out at the University of Arizona in joint work with M. H. Hays and C. D. Levermore. In more recent work with Ole Bang, Prof. Miller has carried out a detailed study of the extended excitations in waveguide arrays in which the nonlinearity is second-order rather than third order. Less power is required to excite the second-order nonlinear response, but this power is shared between two frequencies: a fundamental and a second harmonic. This makes the second-order system more interesting.

    This work is represented in publications [J3], [J9], and [J17].

  4. General Soliton Theory

    Drawing on an observation made during the study of "solitonic" time-dependent potentials for the linear Schrödinger equation, Prof. Miller has shown that the hierarchy of the N-component vector nonlinear Schrödinger equation resides within the Kadomtsev-Petviashvili hierarchy for all N. Moreover, the former hierarchies approximate the latter in the limit of large N. This is interesting because it amounts to an approximation of solutions of 2+1 dimensional integrable equations by simultaneous solutions of two compatible 1+1 dimensional integrable equations.

    In work with N. N. Akhmediev of the Australian National University and P. L. Christiansen of the Technical University of Denmark, Prof. Miller has taken a new approach to the old question of "do colliding solitons pass through one another or exchange identities?" For two different soliton equations, model mechanisms for soliton interactions were introduced and in the context of the models exchanges of conserved quantities among interacting solitons were quantified.

    This work is represented in publications [J5], [J11], [J19], and [J25].

  5. Discrete Systems and Multiscale Phenomena

    This topic represents at the same time Prof. Miller's oldest work and also the motivation for much of his current research. In his earliest work at the University of Arizona with A. C. Scott and others he studied the quantum theory of macromolecules modeled by the quantum discrete nonlinear Schrödinger equation. The main interest was to study the quantum theory of localization and its approximate description via the Hartree approximation.

    The emphasis then shifted from quantum to classical, and also from localized solutions to extended solutions that are slowly modulated plane waves. With M. H. Hays and C. D. Levermore, Prof. Miller studied the modulated wave solutions in a large family of discrete models that contains several discrete versions of the nonlinear Schrödinger equation. At one level, this is really a study of certain local conservation laws that can change type from hyperbolic to elliptic. At another level, it is a study of multiscale phenomena because at microscopic scales the solutions are given by nonlinear plane waves while at macroscopic scales, the conservation laws give the dynamics.

    Among the family of discrete systems Prof. Miller studied was the integrable Ablowitz-Ladik discretization of the nonlinear Schrödinger equation. In joint work with N. Ercolani and C. D. Levermore (then at the University of Arizona) and I. M. Krichever (then at the Landau Institute), Prof. Miller developed the algebraic geometry of the multiphase exact solutions of this integrable model. These solutions generalize the simple plane wave solutions. This work also derives the modulation equations that govern the macroscopic behavior of modulated multiphase waves and analyzes their stability. In another paper, Prof. Miller identified and studied the unusual phenomenon of slow phase modulation that can occur in this model as a consequence of a resonance that is preserved by the modulation equations.

    Prof. Miller has also applied results from the theory of discrete systems to the study of multiple core waveguide arrays in nonlinear optics, as described above (see Nonlinear Waveguide Arrays).

    This work is represented in publications [J1], [J2], [J3], [J4], [J8], [J9], and [J17].

Working Group in Integrable Systems and Asymptotics: Archives

Downloadable Presentations

Click on the number to download a copy.