Large-Degree Asymptotics of Rational Painlevé-II Functions. Noncritical behavior.
Robert J. Buckingham and Peter D. Miller
Department of Mathematical Sciences, University of Cincinnati
Department of Mathematics, University of Michigan, Ann Arbor
Abstract:
Rational solutions of the inhomogeneous Painlevé-II equation and of a related coupled Painlevé-II system have recently arisen in studies of fluid vortices and of the sine-Gordon equation. For the sine-Gordon application in particular it is of interest to understand the large-degree asymptotic behavior of the rational Painlevé-II functions. We explicitly compute the leading-order large-degree asymptotics of these two families of rational functions valid in the whole complex plane with the exception of a neighborhood of a certain piecewise-smooth closed curve. We obtain rigorous error bounds by using the Deift-Zhou nonlinear steepest-descent method for Riemann-Hilbert problems.
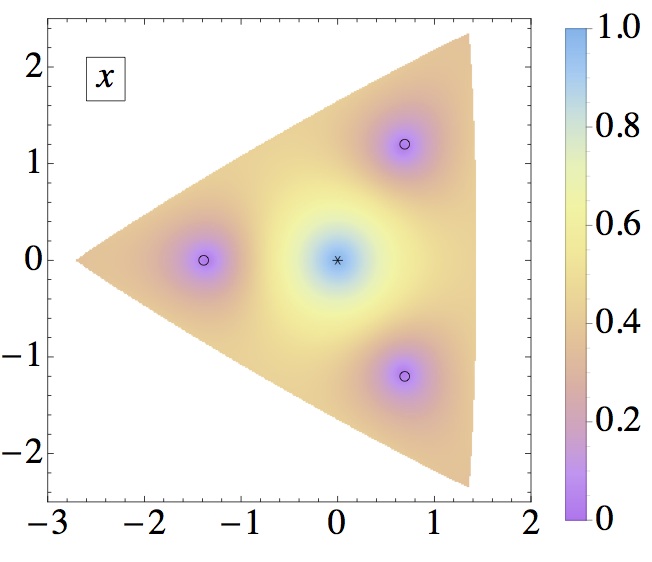
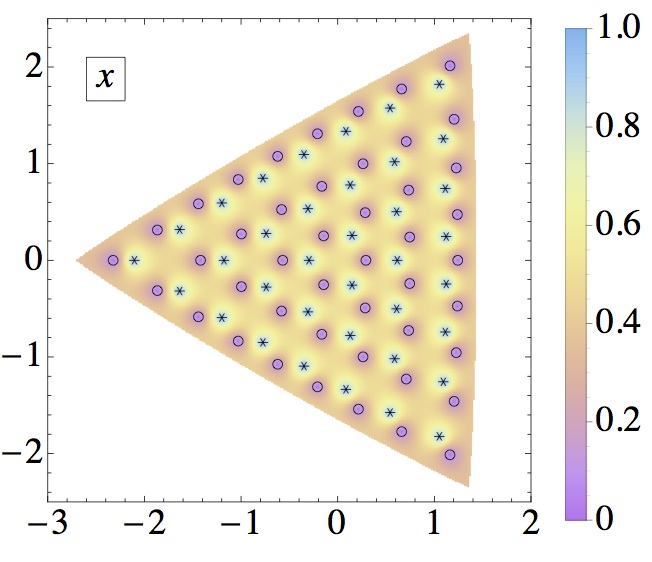
Left: \(m=2\). Right: \(m=9\).