Extreme Superposition: Rogue Waves of Infinite Order and the Painlevé-III Hierarchy
Deniz Bilman, Liming Ling, and Peter D. Miller
Department of Mathematics, University of Michigan
Abstract:
We study the fundamental rogue wave solutions of the focusing nonlinear Schrödinger equation in the limit of large order. Using a recently-proposed Riemann-Hilbert representation of the rogue wave solution of arbitrary order \(k\), we establish the existence of a limiting profile of the rogue wave in the large-\(k\) limit when the solution is viewed in appropriate rescaled variables capturing the near-field region where the solution has the largest amplitude. The limiting profile is a new particular solution of the focusing nonlinear Schrödinger equation in the rescaled variables - the rogue wave of infinite order - which also satisfies ordinary differential equations with respect to space and time. The spatial differential equations are identified with certain members of the Painlevé-III hierarchy. We compute the far-field asymptotic behavior of the near-field limit solution and compare the asymptotic formulae with the exact solution with the help of numerical methods for solving Riemann-Hilbert problems. In a certain transitional region for the asymptotics the near field limit function is described by a specific globally-defined tritronquée solution of the Painlevé-II equation. These properties lead us to regard the rogue wave of infinite order as a new special function.
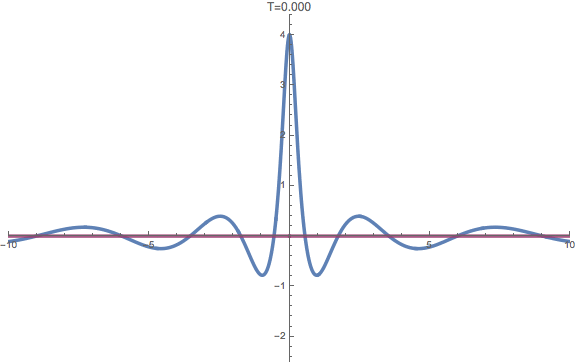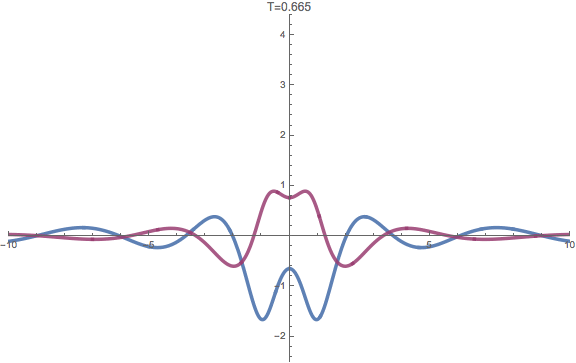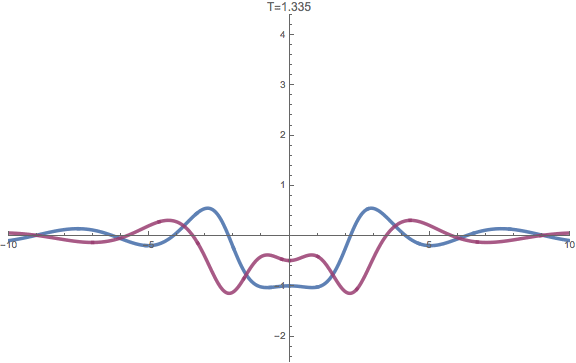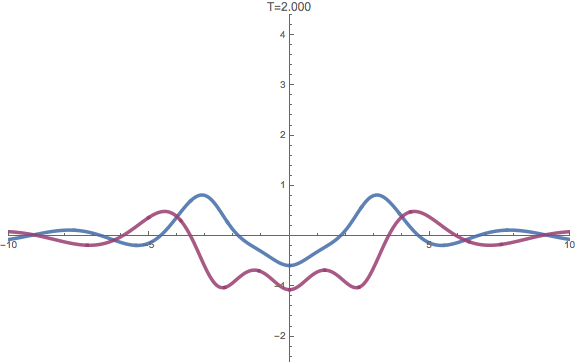
The real and imaginary parts of the rogue wave of infinite order.