Painlevé-III Monodromy Maps Under the \(D_6\to D_8\) Confluence and Applications to the Large-Parameter Asymptotics of Rational Solutions
Ahmad Barhoumi, Oleg Lisovyy, Peter D. Miller, and Andrei Prokhorov
AB, PDM, AP: Department of Mathematics, University of Michigan, Ann Arbor
OL: University of Tours
Abstract:
The third Painlevé equation in its generic form, often referred to as Painlevé-III\((D_6)\), is given by \[ \frac{\mathrm{d}^2u}{\mathrm{d}x^2}=\frac{1}{u}\left(\frac{\mathrm{d}u}{\mathrm{d}x}\right)^2-\frac{1}{x}\frac{\mathrm{d}u}{\mathrm{d}x}+\frac{\alpha u^2+\beta}{x}+4u^3-\frac{4}{u},\quad \alpha,\beta\in\mathbb{C}. \] Starting from a generic initial solution \(u_0(x)\) corresponding to parameters \(\alpha,\beta\), denoted as the triple \((u_0(x),\alpha,\beta)\), we apply an explicit Bäcklund transformation to generate a family of solutions \((u_n(x),\alpha+4n,\beta+4n)\) indexed by \(n\in\mathbb{N})\). We study the large \(n\) behavior of the solutions \((u_n(x),\alpha+4n,\beta+4n)\) under the scaling \(x=z/n\) in two different ways: (a) analyzing the convergence properties of series solutions to the equation, and (b) using a Riemann-Hilbert representation of the solution \(u_n(z/n)\). Our main result is a proof that the limit of solutions \(u_n(z/n)\) exists and is given by a solution of the degenerate Painlevé-III equation, known as Painlevé-III\((D_8)\), \[ \frac{\mathrm{d}^2U}{\mathrm{d}z^2}=\frac{1}{U}\left(\frac{\mathrm{d}U}{\mathrm{d}z}\right)^2-\frac{1}{z}\frac{\mathrm{d}U}{\mathrm{d}z}+\frac{4U^2+4}{z}. \] A notable application of our result is to rational solutions of Painlevé-III\((D_6)\), which are constructed using the seed solution \((1,4m,-4m)\) where \(m\in\mathbb{C}\setminus(\mathbb{Z}+\frac{1}{2})\) and can be written as a particular ratio of Umemura polynomials. We identify the limiting solution in terms of both its initial condition at \(z=0\) when it is well-defined, and by its monodromy data in the general case. Furthermore, as a consequence of our analysis, we deduce the asymptotic behavior of generic solutions of Painlevé-III, both \(D_6\) and \(D_8\) at \(z=0\). We also deduce the large \(n\) behavior of the Umemura polynomials in a neighborhood of \(z=0\).
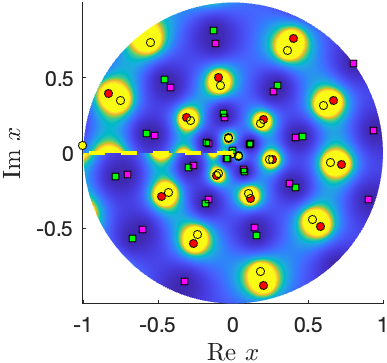
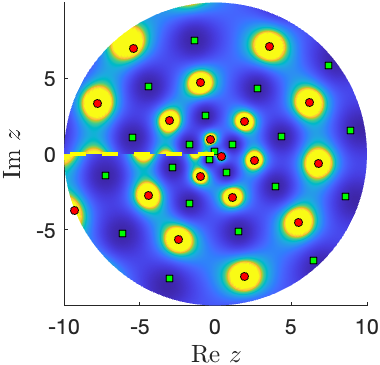
Complex zeros and poles of a large-order Bäcklund-transformed solution of Painlevé-III\((D_6)\) (left) and the limiting solution of Painlevé-III\((D_8)\).