On strong zero-dispersion asymptotics of Benjamin-Ono soliton ensembles
Elliot Blackstone, Louise Gassot, and Peter D. Miller
EB and PDM: Department of Mathematics, University of Michigan, Ann Arbor
LG: CNRS and Department of Mathematics, University of Rennes, France
Abstract:
A soliton ensemble is a particular kind of approximation of the solution of an initial-value problem for an integrable equation by a reflectionless potential that is well adapted to singular asymptotics like the small-dispersion limit. We show how soliton ensembles for the Benjamin-Ono equation can be analyzed in this limit via the construction of local approximations that capture highly oscillatory features of the solution and hence provide more information than weak convergence results that are easier to obtain. These local approximations are deduced from the distributions of eigenvalues of two related matrices, one Hermitian and another non-Hermitian. We perform careful numerical experiments to deduce the asymptotic behavior of the eigenvalues of these matrices in the small-dispersion limit, and formulate conjectures reflecting our observations. Then we apply the conjectures to construct the local approximations of slowly varying profiles and rapidly oscillating profiles as well. We show that the latter profiles are consistent with the predictions of Whitham modulation theory as originally developed for the Benjamin-Ono equation by Dobrokhotov and Krichever.
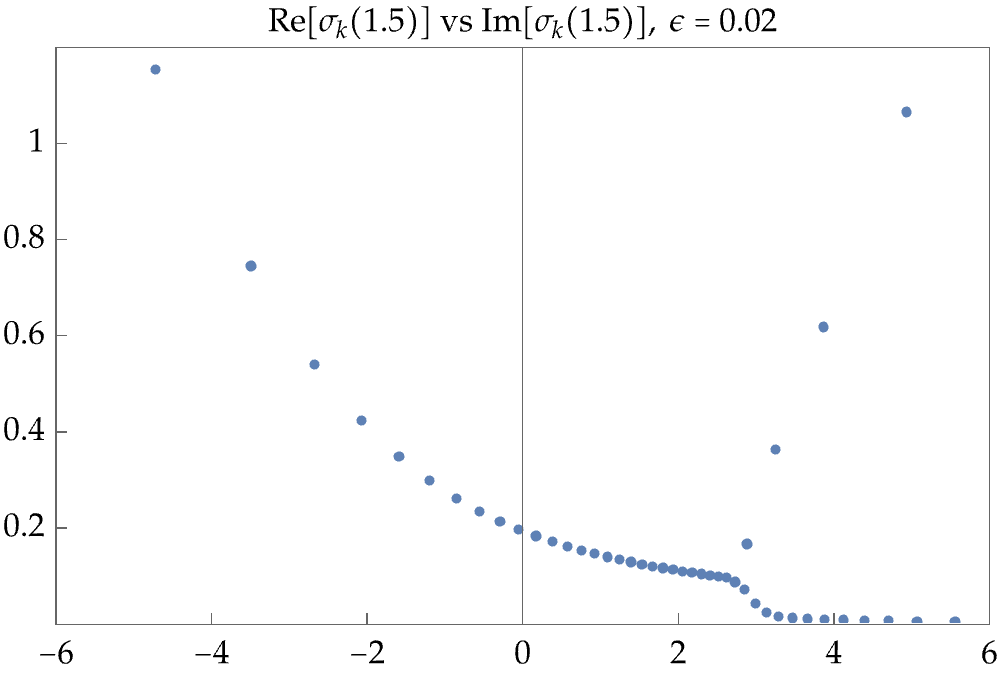

Left: the complex eigenvalues of the non-Hermitian matrix \(\mathbf{C}(1.5)\). Right: the small real eigenvalues of the Hermitian matrix \(\mathbf{A}(x,1.0)\) versus \(x\).