Discrete Orthogonal Polynomials
Discrete Orthogonal Polynomials: Asymptotics and Applications, volume 164 of the Annals of Mathematics Studies
series published by Princeton University Press, is a research monograph jointly authored with Jinho Baik, Thomas Kriecherbauer, and Ken McLaughlin. This book
develops a new method for extracting detailed asymptotic behavior of families of polynomials orthogonal with respect to discrete weights of a rather general form. In particular,
it is shown that asymptotic formulae known to hold for certain very special weights associated with hypergeometric functions actually hold in great generality. These
results may be used to establish universality conjectures for 
discrete analogues of random matrix theory. The asymptotic formulae are used to analyze the problem of random
tilings of hexagons with rhombus tiles and also to provide new results for the continuum limit of the Toda lattice.
Update Log
Here you will be able to find a complete listing of updates to the published text, as they become known.
Movie
Each frame of this movie shows a plot of a scaled version of the orthogonal polynomial of degree 25 in a system of polynomials orthogonal with respect to the discrete weight obtained by sampling a continuous weight associated with the potential tx + cos(2πx)/2 on a grid of 40 points in the interval (0,1) distributed with density proportional to 1+10x. The frames of the movie are parametrized by the variable t, which is the "time" of the Toda flow.
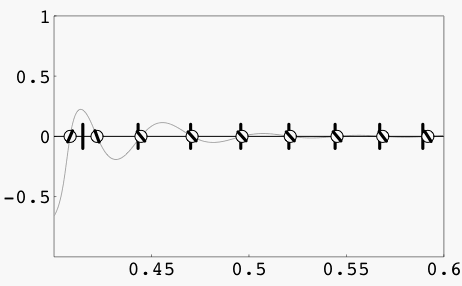
Just click on the image to begin the movie!
The tick marks on the x-axis are the discrete nodes of orthogonality, and the circles are centered at the zeros of the orthogonal polynomial. The angle of the slash within each circle indicates the location of the zero within the interval between two neighboring nodes. The angle is only discontinuous at the nodes, so a sudden jump in the angle indicates a zero passing through a node.