The Benjamin-Ono equation in the zero-dispersion limit for rational initial data: generation of dispersive shock waves
Elliot Blackstone, Louise Gassot, Patrick Gérard, and Peter D. Miller
EB and PDM: Department of Mathematics, University of Michigan, Ann Arbor
LG: CNRS and Department of Mathematics, University of Rennes, Rennes, France
PG: Laboratoire de Mathématiques d'Orsay, Université Paris-Saclay, Orsay, France
Abstract:
The leading-order asymptotic behavior of the solution of the Cauchy initial-value problem for the Benjamin-Ono equation in \(L^2(\mathbb{R})\) is obtained explicitly for generic rational initial data \(u_0\). An explicit asymptotic wave profile \(u^\mathrm{ZD}(t, x; \epsilon)\) is given, in terms of the branches of the multivalued solution of the inviscid Burgers equation with initial data \(u_0\), such that the solution \(u(t, x; \epsilon)\) of the Benjamin-Ono equation with dispersion parameter \(\epsilon > 0\) and initial data \(u_0\) satisfies \(u(t, x; \epsilon) - u^\mathrm{ZD}(t, x; \epsilon) \to 0\) in the locally uniform sense as \(\epsilon\to 0\), provided a discriminant inequality holds implying that certain caustic curves in the \((t, x)\)-plane are avoided. In some cases this convergence implies strong \(L^2(\mathbb{R})\) convergence. The asymptotic profile \(u^\mathrm{ZD}(t, x;\epsilon)\) is consistent with the modulated multi-phase wave solutions described by Dobrokhotov and Krichever.
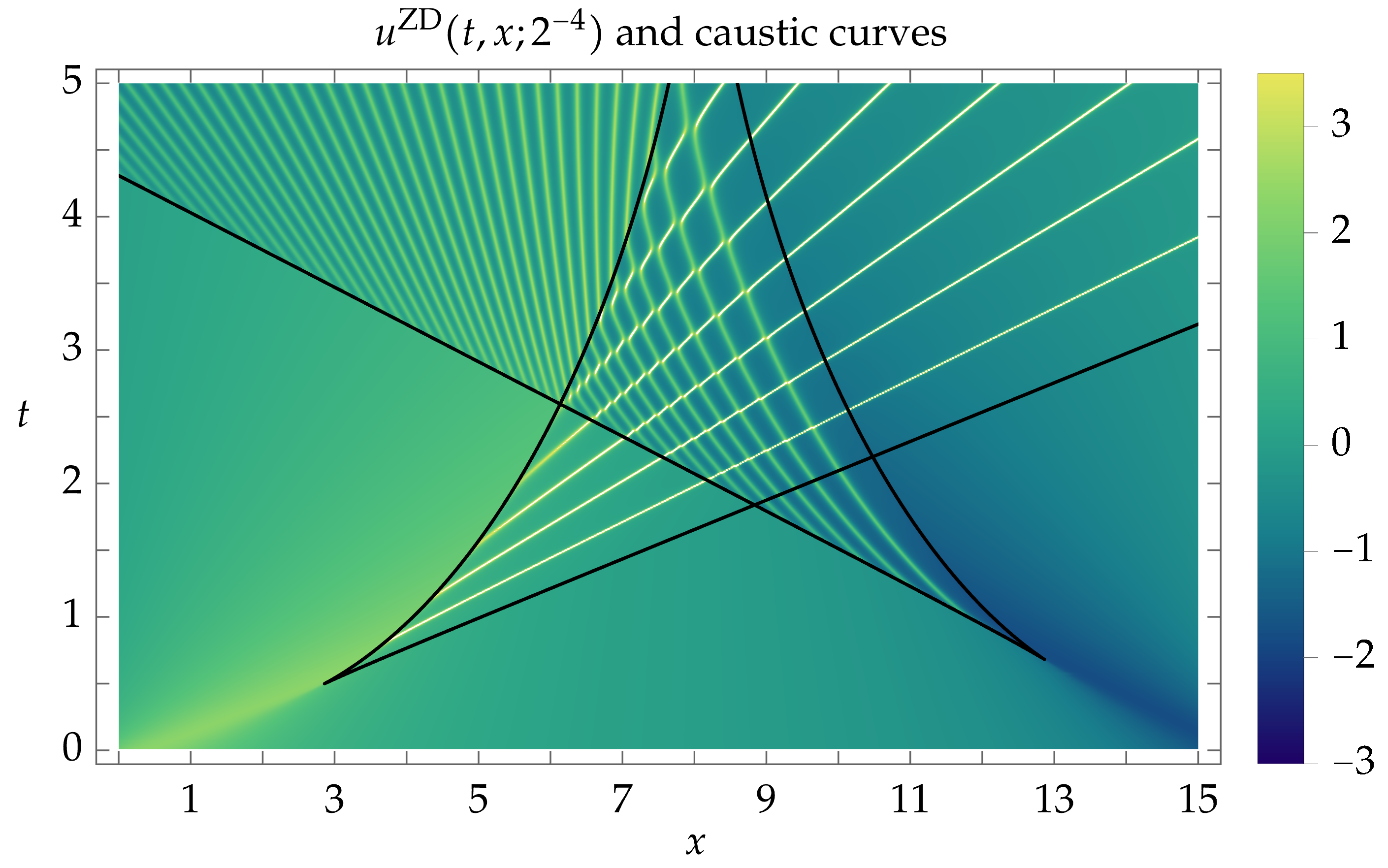
The explicit approxmation \(u^\mathrm{ZD}(t,x;2^{-4})\).