Mathematics: a branch of physics in
which the
experiments are cheap.
--V. I. Arnold [not an exact quote]
Archive of Research Data And Other Useful Stuff
Coxeter Planes
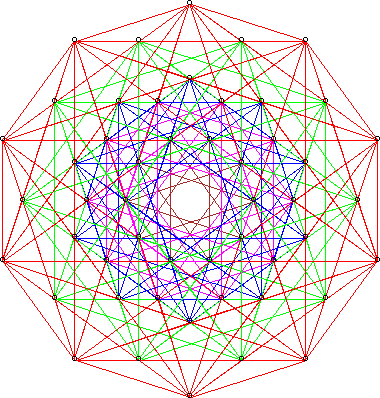
There is a canonical two-dimensional subspace associated to
any root system or reflection group; namely, one where a
Coxeter element acts as rotation by 2Pi/h, where
h denotes the Coxeter number.
Check out the interesting graphic images
obtained by projecting the root system into this plane.
By popular demand, I've added
some more graphic images obtained by
projecting regular 4D-polytopes into their Coxeter planes.
For starters, here's the projection of the root system of D6
into its Coxeter plane:
Explicit Matrices for Irreps of Weyl Groups
In connection with the
Atlas of Lie Groups Project, I've constructed a database of explicit
matrices for every irreducible representation of every Weyl group of
rank <= 8. The matrices are provided in a collection of highly compressed
text files suitable for reading into a Maple session.
The database should work with all versions of Maple.
The Kontsevich conjecture
In support of my paper
Counting points on varieties over finite fields related to
a conjecture of Kontsevich [PDF], I'm releasing a collection
of Maple programs and data. The programs can be used to
explicitly count the number of zeroes of a set of multivariate
polynomials over the finite field GF(q),
treating q as an indeterminate.
There must be a catch, you say.
Well, yes. The catch is that the program only works well when the
polynomials have a very special form. Typically, you need many of
the variables to occur linearly in the polynomials (e.g., sums of
square-free monomials). And that's just for starters.
Kontsevich's conjecture says that if you take the generating
function for all spanning trees of a graph (one variable for each edge),
then the number of zeroes in GF(q) should be a polynomial
in q. So along with the programs, there are several files of
graphs that meet necessary conditions for a minimal counterexample
to Kontsevich's conjecture and some related conjectures. If you want
more details, you'll have to read the paper and the documentation.
This gzipped tar file has everything you need:
reduce.tar.gz (24K).
Here's an overview of what's inside:
READ_ME.
The Fine Print: All of the above should work with Maple V
Releases 3, 4, 5.
Update [4-Sep-2009]: We've updated the software so that
it should run in more recent versions of Maple, and to fix a bug
found by Oliver Schnetz. See also
Schnetz's paper
in the Archive -- he discovered that the smallest counterexamples to
the Kontsevich conjecture have 14 edges.
Coxeter graph paper
If you've ever worked with affine reflection groups, you've probably
wasted lots of time drawing the reflecting hyperplanes of the rank 2
groups on scraps of paper. You may also have wished you had pads of
graph paper with these lines drawn in for you. If so, you've come to
the right place. Behold! Coxeter graph paper!
Want more? Check out
affhyp (
recently updated for Maple VR4), the Maple program that produced this paper.
Requires the coxeter package. Affhyp can do lots more--here
are some samples of snazzy 3D graphics it produced:
- The hyperplanes corresponding to the root systems
A3 (27K gif) and
B3 (23K gif).
- The "sandwich" arrangements for
A3 (27K gif),
B3 (27K gif), and
C3 (26K gif).
Poset lists
For the benefit of those of you who cannot use my posets
package, here are the lists of posets on 8 or fewer vertices.
The larger files are gzip images of plain text files, suitable for
reading into a Maple session. If you are skilled in the use of a text
editor, you can transform these files into any format you like.
A description of the format appears at the top of each file.
Jack symmetric functions
These files contain tables of Jack's symmetric functions up to degree 16,
in a highly compressed format. Each file is the gzip image of a plain
text file, suitable for reading into a Maple session. Requires
the SF package.
In order to use this data, you'll need
jacktools, a Maple program for installing
the data in these tables into an SF session. The tables were
built using this code from the
SF package.
It takes about 10 minutes to build these tables on a 2.4 GHz P4
running Maple 9 on Linux.
q,t-Kostka polynomials
These files contain tables of q,t-Kostka polynomials up to degree 10,
created with the SF package. Each file is the gzip image of a plain
text file suitable for reading into a Maple session.
Back to John Stembridge's Home Page
This page last modified
Sun Aug 4 19:50:02 EDT 2024
