Math 594: Algebra II

Professor: David E Speyer

Winter 2017

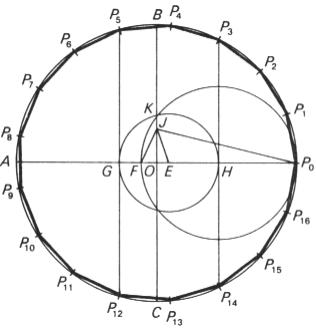
History (somewhat idealized) and Overview: Since ancient Babylon and Greece, mathematicians have developed methods to solve systems of equations. In the final years of the eighteenth century, mathematicians began to suspect that their tools were fundamentally incapable of solving certain equations: Gauss (1796) asserted that the coordinates of a regular heptagon could not be found by straightedge and compass, and Ruffini (1799) gave an incomplete proof that the roots of a general quintic polynomial could not be computed by basic arithmetic operations. A few decades after these questions were formally asked, they were answered. Abel (1832) proved Ruffini's claim and Wantzel (1837) proved Gauss's. In 1846, Galois invented what is now known as Galois theory, which clarified Abel and Wantzel's results and permitted many new ones. From Galois's perspective, Galois theory was a tool to systematically analyze the process of extracting roots of equations. In modern mathematics, it is a crucial tool in number theory, algebraic geometry and commutative algebra, as well as still being relevant to its original purpose. The subject of this course is Galois theory and the topics which lead up to Galois theory. Specifically, we will discuss group theory and field theory, and then move to the beauties of Galois theory itself. Linear algebra could also be considered a topic leading into Galois theory. As abstract linear algebra is a prerequisite for this course, we will not cover it as a separate subject, but we will certainly use linear algebra often and I expect many of you will improve your knowledge of it.

Text: Milne's notes Group Theory and Fields and Galois Theory.

Office hours My office hours will be 1-2:30 on Wednesdays and 11:30-1:00 on Thursdays.

Professor: David E Speyer, 2844 East Hall, speyer@umich.edu

Course homepage: http://www.math.lsa.umich.edu/~speyer/594

Level: Graduate students and advanced undergraduates.

Prerequisites: Prior exposure to the definitions of groups, rings, modules and fields. Abstract linear algebra over an arbitrary field. Principal ideal domains (PIDs) and unique factorization. 513 and 593 are enough background; please speak to me if you have questions about your background.

Student work expected: I will give problem sets every week, due on Tuesdays Thursdays.

Homework Policy: You are welcome to consult your class notes and textbook.

You are welcome to work together with your classmates provided (1) you list all people and sources who aided you, or whom you aided and (2) you write-up the solutions independently, in your own language. If you seek help from mathematicians/math students outside the course, you should be seeking general advice, not specific solutions, and must disclose this help. I am, of course, glad to provide help!

I do not intend for you to need to consult other sources, printed or online. If you do consult such, you should be looking for better/other expositions of the material, not solutions to specific problems. In particular, I will assign many standard lemmas which will be valuable for you to prove for yourselves; searching for other people's proofs of these results would be self-defeating.

You MAY NOT post homework problems to internet fora seeking solutions. Although I know of cases where such fora are valuable, and I participate in some, I feel that they have a major tendency to be too explicit in their help. You may post questions asking for clarifications and alternate perspectives on concepts and results we have covered.

Problem Sets

Topics covered