Math 594: Algebra II
Professor: David E Speyer
Winter 2022
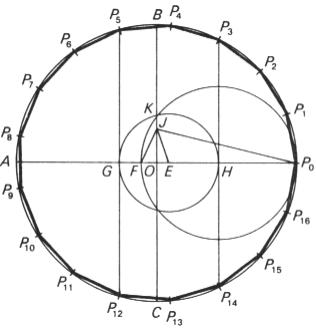
Gauss's construction of the regular heptadecagon
Course meets: Tuesday and Thursday, 10-11:30 AM, 4088 East Hall.
Office hours: 2844 East Hall, Tuesdays 2-5 PM, Thursdays 12-3
PM. At the moment I am planning to have all office hours open to all my courses;
if this is a problem, we'll adjust. If you'd like to meet on Zoom, send an e-mail and I'll be glad to log on.
Professor: David E Speyer, 2844 East Hall, speyer@umich.edu
Course homepage: http://www.math.lsa.umich.edu/~speyer/594
Level: Graduate students and advanced undergraduates.
Prerequisites: Prior exposure to the definitions of groups,
rings, modules and fields, at the level of 593 or a similar course. Abstract linear algebra over an arbitrary
field.
Structure of class: This class will be taught in an IBL style,
meaning that a large portion of the class time will be spent solving
problems that develop the theory we are studying. Students are expected to
attend class and participate in solving problems, as the class will not
work otherwise. Some portion of your grade will be allocated for
participation in class work.
Climate: Each of you deserves to learn in an environment where
you feel safe and respected.
I want our classroom, the collaborations between my students outside
class, and our department as a whole, to be an environment where
students feel able to share their ideas, including those which are
imperfectly formed, and where we will respectfully help each other
develop our understanding. I want to provide a space where questions
are very welcome, especially on basic points.
Please ask all questions you have; remember that every question you
have is likely a question that many share. Please share your insights
and suggestions, partial or complete. Please treat your peers
questions, comments and ideas with respect.
Homework: I will assign weekly problem sets, due on
Tuesday nights at midnight (through Gradescope).
QR practice: Most students in this class are
preparing to take the QR exam in algebra. This course will cover the
vast bulk of the material from the Algebra
1 syllabus (and more).
Each week, I will assign a timed quiz on Gradescope
consisting of two QR questions, on topics related to the current class
material, to be done within a one hour period. See below for quiz policies.
Grading: A numerical score will be computed as follows:
- 50% homeworks not including the write ups of class problems, with the lowest two weeks dropped
- 30% write ups of class problems, with the lowest two weeks dropped
- 10% QR practice quizzes, with the lowest six weeks dropped
- 10% Class participation
These numerical scores will be converted into letter grades
Weekly assignments
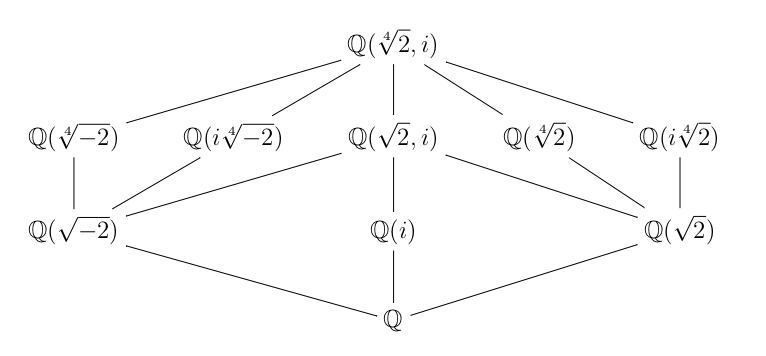
The intermediate fields of a dihedral extension
Homework PoliciesYou are welcome to work together with your classmates provided (1) you
list all people and sources who aided you, or whom you aided and (2)
you write-up the solutions independently, in your own language. If you
seek help from mathematicians/math students outside the course, you
should be seeking general advice, not specific solutions, and must
disclose this help. I am, of course, glad to provide help!
I do not intend for you to need to consult other sources, printed or
online. If you do consult such, you should be looking for better/other
expositions of the material, not solutions to specific problems. Math
problems are often called "exercises"; note that you cannot get
stronger by watching someone else exercise!
You MAY NOT post homework problems to internet fora seeking
solutions. Although I know of cases where such fora are valuable, and
I participate in some, I feel that they have a major tendency to be
too explicit in their help. You may post questions asking for
clarifications and alternate perspectives on concepts and results we
have covered.
Quiz policies Just as on the QR exams, please schedule a single uninterrupted
time period to take this quiz and please complete the quiz
without aid of any other resources, including written notes, internet
references or other people.
I hope and believe that this practice will be useful beyond the QR
exam. I think that the ability to solve problems which take 5-20
minutes is what unlocks the ability to solve problems that take months
or years. I should say that this is something where different
mathematicians experience varies wildly: I have found my ability to
prove and disprove minor claims quickly has been extremely helpful in
letting me explore difficult areas without getting lost; other
mathematicians whom I greatly respect disagree. I hope that giving you
some practice in this skill will be at least of some help.
I also encourage students to attempt other past QR exams. I am glad to discuss problems on these exams with you.
Problem Sets
Problem sets will generally be due at midnight (or, more precisely,
11:59 PM) between Tuesday and Wednesday.
The first practice QR
quiz will be due January 25.
- Problem Set 1 (LaTeX), due 11:59 PM on January 18.
- Problem Set 2 (LaTeX), due 11:59 PM on January 25.
- Problem Set 3 (LaTeX), due 11:59 PM on February 1.
- Problem Set 4 (LaTeX), due 11:59 PM on February 8.
- Problem Set 5 (LaTeX), due 11:59 PM on
February 15February 16.
- Problem Set 6 (LaTeX), due 11:59 PM on February 22.
- Problem Set 7 (LaTeX), due 11:59 PM on March 15 (no problem set is due on March 1 or 8).
- Problem Set 8 (LaTeX), due 11:59 PM on March 22.
- Problem Set 8 (LaTeX), due 11:59 PM on March 22.
- Problem Set 9 (LaTeX), due 11:59 PM on March 29.
- Problem Set 10 (LaTeX), due 11:59 PM on April 5.
- Problem Set 11 (LaTeX), due 11:59 PM on April 12. This is the final problem set!
Class schedule and worksheets
These worksheets are written by David E Speyer and released under a Creative
Commons By-NC-SA 4.0 International License.
Here are all the worksheets in a single file.
Below are the worksheets which we have used so far, and the worksheets
which I anticipate using in the next few days. Feel free to look ahead
at future worksheets before class. I do not promise to follow this
schedule, but it is my best estimate.
- January 6: The
quadratic, cubic and quartic formulas and worksheet on symmetries of
polynomials.
- Jan 6: Introductory lecture on the quadratic, cubic and
quartic formulas, plus solutions to problems 1.1-1.3 and
1.4.(1). We'll discuss 1.4.(2) and 1.4.(3) next time and skip 1.5.
- January 11: Characters of
symmetric groups.
- Jan 11: All problems solved. We have now classified the
characters of Sn and An.
- January 13: A weak version
of the unsolvability of the quintic.
- Jan 13: We proved the theorem! We now know that, if
there is a quintic formula, it has to step outside the world of
rational functions in the roots.
- January 18: Groups.
- Jan 18: Not only did we solve all the problems on the Groups Worksheet, through a combination of lecture and student solutions, we solved all problems on Group actions except for proving Burnside's lemma. Burnside's lemma will be moved to problem sets so that we can move on.
- January 20: Normal subgroups.
- Jan 20: Problems 6.1-6.5 proved in class discussion. Many
additional conditions, equivalent to N being normal, were proposed,
such as (4') gN = Ng for all g in G (6) gNhN = ghN for all g and h in
G (7) there is a group structure on G/N such that g → gN is
a group homomorphism and (8) there is a group homomorphism G → H
with kernel N. We won't do 6.6-6.8; please do read the definition of a short exact sequence.
- January 25: Simple groups. I also hope to spend a bit of time talking more about normal subgroups, stabilizers and conjugacy classes.
- Jan 25: Problems 7.1-7.3 solved easily. Problem 7.4 solved partly in groups and partly at end of class. If I get a chance, I'll write up some notes on this argument, because it was a little rushed. In the mean time, here are Keith Conrad's Five proofs that An is simple. The argument I gave is mostly his second proof, but replacing the slick tricks to check A5 and A6 with brute force.
- January 27-February 1: Subnormal series and composition series. Many minor edits have been made to worksheet for consistency.
- Jan. 27: Problems 8.1-8.4 solved cleanly. 8.5 mostly solved but wrapping up as we ended; 8.6 in progress in most groups. We'll shuffle groups next time and resume.
- Feb. 1: The remaining results were proved.
- February 3: The Jordan-Holder theorem for groups
- Feb 3: Good class! All problems were solved!
- February 8: Solvable groups
- Feb 3: Good class! All problems but the last were solved. We'll leave the symmetric group problems for you to do on your own; they are basically the computations from Worksheet 2 in more sophisticated language.
- February 10: Discussion of previous QR quizzes and, if time permits, Nilpotent groups
- Feb 10: Good discussion of quiz problems, and we started nilpotent groups. I am going to postpone the nilpotent groups worksheet until later and move most of it to the problem sets.
- February 15-17: Direct products and start Semidirect products
- Feb 15: All problems except 11.6 solved on direct products. 12.1-12.3 solved on semidirect products, and everyone understands that 12.4 would just be a matter of slogging through. We'll start with 12.5 next time.
- Feb 17: We discussed semidirect products for a while, before moving to the worksheet. Problems 12.5 and 12.6 were solved in both groups; Problem 12.7.(1) was presented on the blackboard. We'll move on.
- February 22: Abelian extensions
- Feb 22: Problems 13.1-13.7 solved in the course of lecture. Problem 13.8 was in progress and will be solved next time.Problems 13.9-13.10 will migrate to homework.
- February 24: Catch up and prove the abelian Schur-Zassenhaus
theorem (lecture). Our approach is closely based on Kurzweil and Stellmacher, The Theory of Finite Groups, Chapter 3.3. Here are the worksheets I had prepared (the second one would have come after the Sylow theorems): The Schur-Zassenhaus theorem (abelian case), The Schur-Zassenhaus theorem (general case)
- SPRING BREAK
- March 8-10: The Sylow theorems.
- Mar. 8: We proved Sylow theorems I and II. We will prove Sylow III on Thursday.
- Mar. 10: We proved Sylow III in class discussion.
- March 10: Applications of the Sylow theorems.
- Mar. 10: Problems 15.5-15.7 done in class, others will appear on homework. Although I'd love to do more, we need to start field theory. Here is a worksheet that had to be skipped: Nilpotent groups are product of p-groups.
- March 15: Field theory begins. We'll do Review of Polynomial Rings quickly and Degrees of Field Extensions and Constructible Numbers.
- Mar 15: All problems solved on both worksheets (except for computing the minimial polynomial of cos 20).
- March 17-March 22: Splitting fields and the maps between them.
- Mar 17: Problems 18.1 and 18.2 done in lecture, 18.3, 18.4 and 18.5 done in small groups. 18.5 created a lot of discussion; I made some edits to the work sheet which I hope might help. We'll return to 18.6 and 18.7 next time.
- Mar 22: Problems 18.6 and 18.7 done on board.
- March 22: Introduction to field automorphisms.
- Mar 22: Problems 19.1-19.3 solved; problem 19.4 on board. We'll wrap up Problem 19.5 next time.
- March 24: Galois extensions
- Mar 24: Problem 19.5 and 20.1-20.3 solved in groups; 20.4 presented by Prof. Speyer on board.
- March 29-31: Towers of Galois extensions
- Mar 29: Great class! Problems 21.1-21.7 solved. Problem 21.8 will be presented at the start of Thursday's class.
- Mar 29: Radical extensions, solvable groups and the unsolvability of the quintic
(lecture)
- April 5: Artin's lemma
- Apr 5: Great class! All results proved with plenty of time, and we got to the main application, proving the Galois correspondence.
- April 7: Galois closures, thinking about Galois extension (lecture). Here is the previously prepared worksheet on The fundamental theorem of Galois theory
- April 12: Examples (lecture)
- Apr. 12: We worked through the following examples: The splitting field of xn-1 over a general field, the splitting field of xn-c over a general field, the splitting field of x3-2 over the rationals, the splitting field of x4-2 over the rationals, adjoining
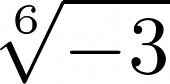 to the rationals, adjoining
to the rationals, adjoining 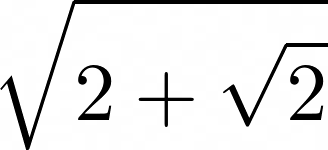 to the rationals.
to the rationals.
- April 14-19: Kummer's theorem, solvable groups come from radical extensions
- Apr 14: Problems 23.1-23.4 solved. I swapped out the proof of
Problem 23.3 for a slicker one as discussed in class, and also
edited the rest of the problem set to address issues raised in class.
- Apr 19: All problems solved, course complete!



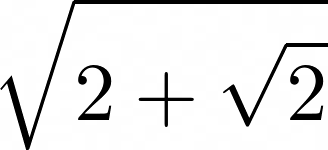 to the rationals.
to the rationals.